Poisson Distribution Formula and Meaning in Finance

Poisson Distribution Formula and Meaning in Finance

The Poisson distribution is a probability distribution that is often used in finance to model the occurrence of rare events. It is named after the French mathematician Siméon Denis Poisson, who first introduced the distribution in the early 19th century.

The Poisson distribution is particularly useful in finance because it allows us to calculate the probability of a certain number of events occurring within a given time period, given the average rate at which the events occur. This can be applied to various financial scenarios, such as predicting the number of customer arrivals at a bank or the number of credit card fraud cases in a month.

The formula for the Poisson distribution is as follows:

P(x; λ) = (e^(-λ) * λ^x) / x!

Where:

• P(x; λ) is the probability of x events occurring
• e is the base of the natural logarithm (approximately 2.71828)
• λ is the average rate at which the events occur
• x is the number of events
• x! is the factorial of x

By plugging in the appropriate values for λ and x into the formula, we can calculate the probability of a specific number of events occurring. This can be useful in financial decision-making, risk management, and other areas of finance where the occurrence of rare events needs to be considered.

It is important to note that the Poisson distribution has certain assumptions and limitations. For example, it assumes that the events occur independently of each other and at a constant rate. In reality, this may not always be the case in financial scenarios. Additionally, the Poisson distribution is most accurate when the average rate of events is relatively small compared to the total number of possible events.

The Poisson distribution is a probability distribution that is used to model the number of events that occur within a fixed interval of time or space. It is named after the French mathematician Siméon Denis Poisson, who first introduced it in the early 19th century.

The Poisson distribution is characterized by a single parameter, λ (lambda), which represents the average rate at which events occur. The probability mass function of the Poisson distribution is given by the formula:

P(x) = (e^(-λ) * λ^x) / x!

Where:

• P(x) is the probability of observing x events
• e is the base of the natural logarithm (approximately equal to 2.71828)
• λ is the average rate at which events occur
• x is the number of events
• x! is the factorial of x

One of the key properties of the Poisson distribution is that the variance is equal to the mean, which means that the distribution is fully determined by its average rate parameter. This property makes it a convenient choice for modeling rare events in finance, where the occurrence of such events is often unpredictable.

However, it is important to note that the Poisson distribution has certain limitations and assumptions. It assumes that the events occur independently of each other and at a constant average rate, which may not always hold true in real-world financial scenarios. Additionally, the Poisson distribution is only appropriate for modeling events that are rare and discrete, and may not be suitable for continuous variables or events that occur frequently.

Applications of the Poisson Distribution in Finance

The Poisson distribution is a mathematical concept that is widely used in finance to model and analyze various phenomena. It is particularly useful in situations where events occur randomly and independently over a fixed interval of time or space.

One of the key applications of the Poisson distribution in finance is in modeling the arrival of customer orders or trades. For example, in a stock market, the number of trades that occur within a given time period can be modeled using a Poisson distribution. This information is valuable for traders and investors who need to understand the frequency and intensity of trading activity in order to make informed decisions.

The Poisson distribution is also used in insurance and risk management. Insurers rely on the Poisson distribution to model the frequency of insurance claims. This helps them determine the appropriate premium rates to charge policyholders and manage their risk exposure. Additionally, the Poisson distribution is used to model the occurrence of rare events, such as natural disasters or catastrophic events, which can have significant financial implications for insurance companies.

Furthermore, the Poisson distribution is used in the field of quantitative finance to model the price movements of financial assets. By assuming that price changes occur randomly and independently, financial analysts and traders can use the Poisson distribution to estimate the probability of certain price movements and assess the risk associated with different investment strategies.

Calculating the Poisson Distribution in Finance

The Poisson distribution is a mathematical concept that is widely used in finance to model the occurrence of rare events. It allows us to calculate the probability of a certain number of events happening within a given time period, based on the average rate of occurrence.

Formula

The formula for calculating the Poisson distribution is as follows:

P(x) = (e^(-λ) * λ^x) / x!

Where:

• P(x) is the probability of x events occurring
• e is the base of the natural logarithm (approximately 2.71828)
• λ is the average rate of occurrence of the events
• x is the number of events
• x! is the factorial of x

Meaning in Finance

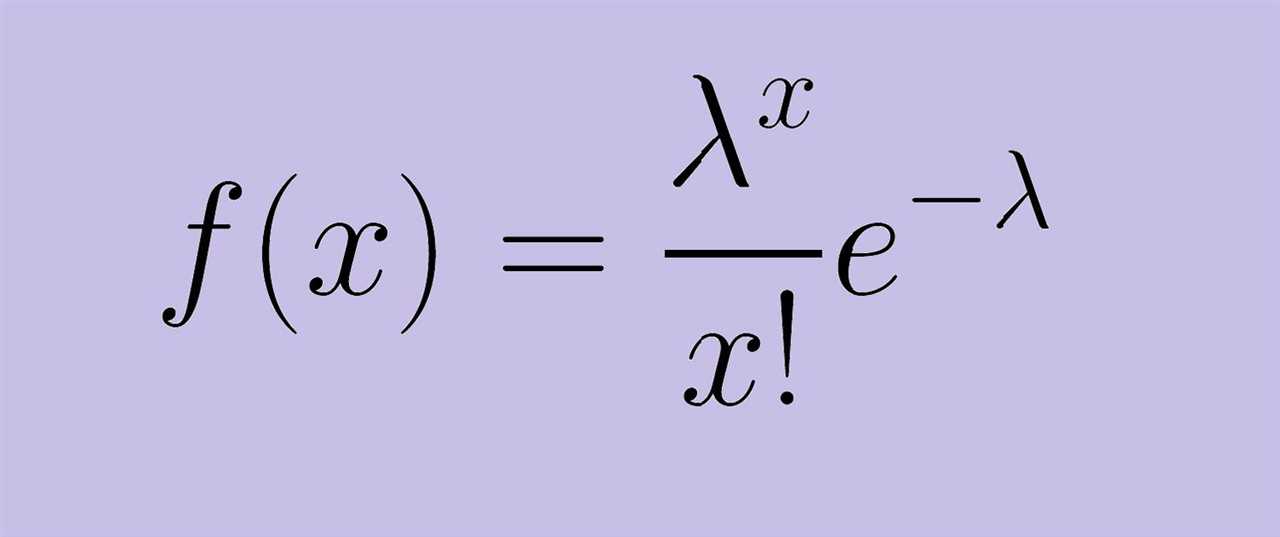
For example, a bank may use the Poisson distribution to determine the number of tellers needed during peak hours to ensure efficient customer service. By analyzing historical data and calculating the average rate of customer arrivals, the bank can estimate the probability of a certain number of customers arriving within a specific time frame and adjust its staffing accordingly.

Steps to Calculate the Poisson Distribution

To calculate the Poisson distribution in finance, follow these steps:

1. Determine the average rate of occurrence (λ) based on historical data or assumptions.
2. Identify the number of events (x) for which you want to calculate the probability.
3. Calculate the factorial of x (x!).
4. Plug the values of λ, x, and x! into the Poisson distribution formula.
5. Calculate the probability (P(x)) using the formula.

By following these steps, you can obtain the probability of a specific number of events occurring within a given time period, which can be valuable for financial analysis and decision-making.

It is important to note that the Poisson distribution assumes that the events occur independently and at a constant average rate. Therefore, it may not be suitable for situations where these assumptions do not hold, such as in highly volatile markets or during periods of significant economic uncertainty.

Limitations and Considerations of the Poisson Distribution in Finance

The Poisson distribution is a useful tool in finance for modeling events that occur randomly and independently over a fixed interval of time or space. However, it is important to understand the limitations and considerations of using the Poisson distribution in financial analysis.

1. Assumption of Independence

One of the key assumptions of the Poisson distribution is that the events being modeled occur independently of each other. In finance, this assumption may not always hold true. For example, in the stock market, the occurrence of one event may affect the probability of other events occurring. Therefore, it is important to carefully consider the independence assumption when using the Poisson distribution in financial modeling.

2. Fixed Interval

The Poisson distribution assumes that the events being modeled occur over a fixed interval of time or space. In finance, this may not always be the case. For example, stock market returns may follow a Poisson distribution over a daily interval, but not necessarily over a monthly or yearly interval. It is important to choose the appropriate interval for the financial analysis and adjust the parameters of the Poisson distribution accordingly.

3. Rare Events

The Poisson distribution is often used to model rare events, where the probability of occurrence is low. In finance, however, rare events may have significant impacts on the market. For example, a financial crisis or a major economic event can have a profound effect on stock prices. In such cases, the Poisson distribution may not accurately capture the extreme events and their associated probabilities.

4. Stationarity

The Poisson distribution assumes that the underlying process generating the events is stationary, meaning that the average rate of occurrence remains constant over time. In finance, this assumption may not hold true, as market conditions and investor behavior can change over time. It is important to consider the non-stationarity of financial data and adjust the parameters of the Poisson distribution accordingly.