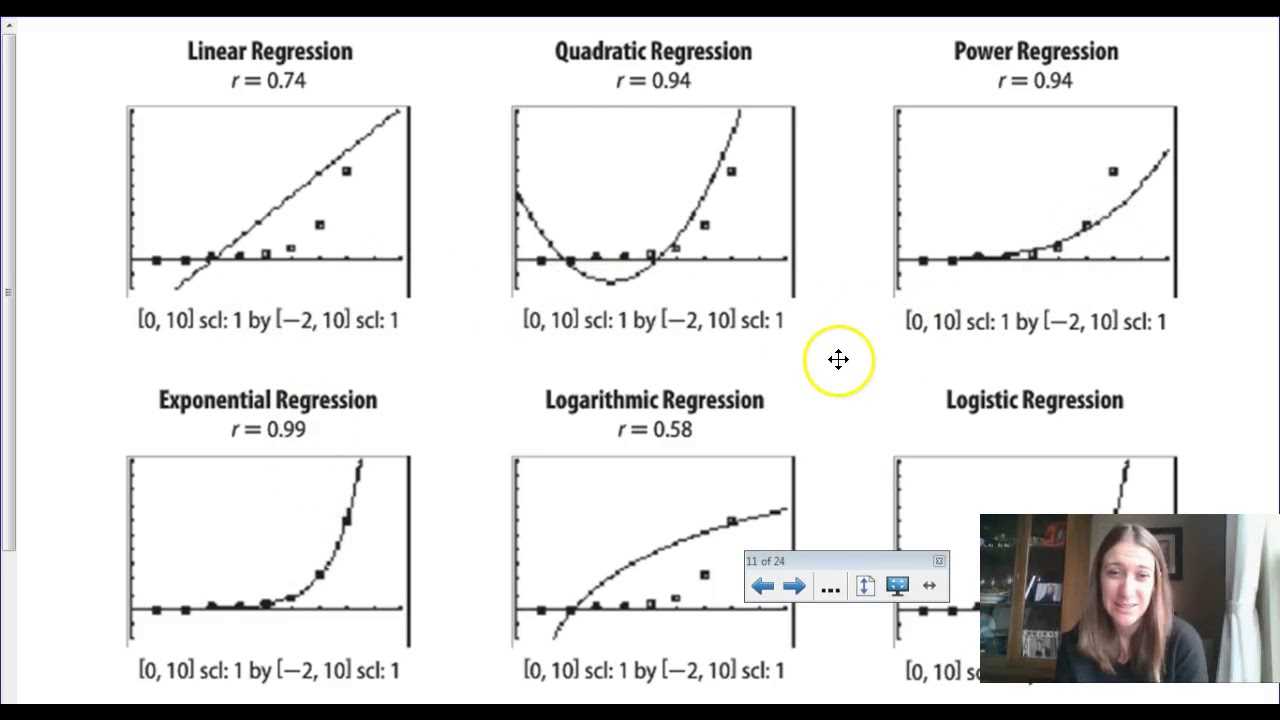
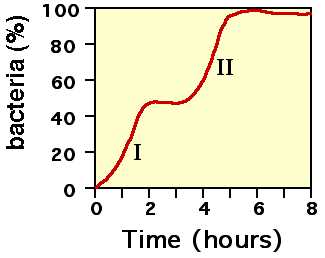
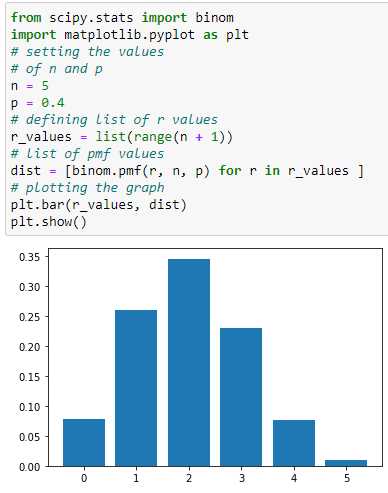
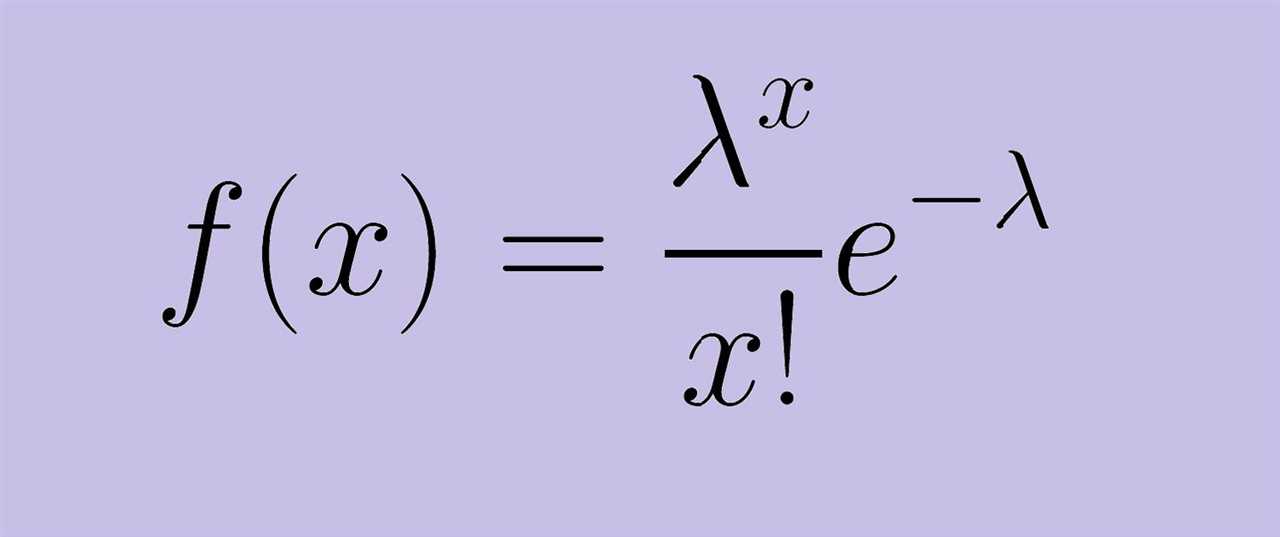Understanding the Uniform Distribution and its Applications
What is the Uniform Distribution? The uniform distribution is a probability distribution that describes a random variable with a continuous and uniform probability density function. In simpler terms, it is a distribution where all outcomes are equally likely. Characteristics of the Uniform Distribution There are a few key characteristics of … …