Money-Weighted Rate of Return Definition Formula and Example

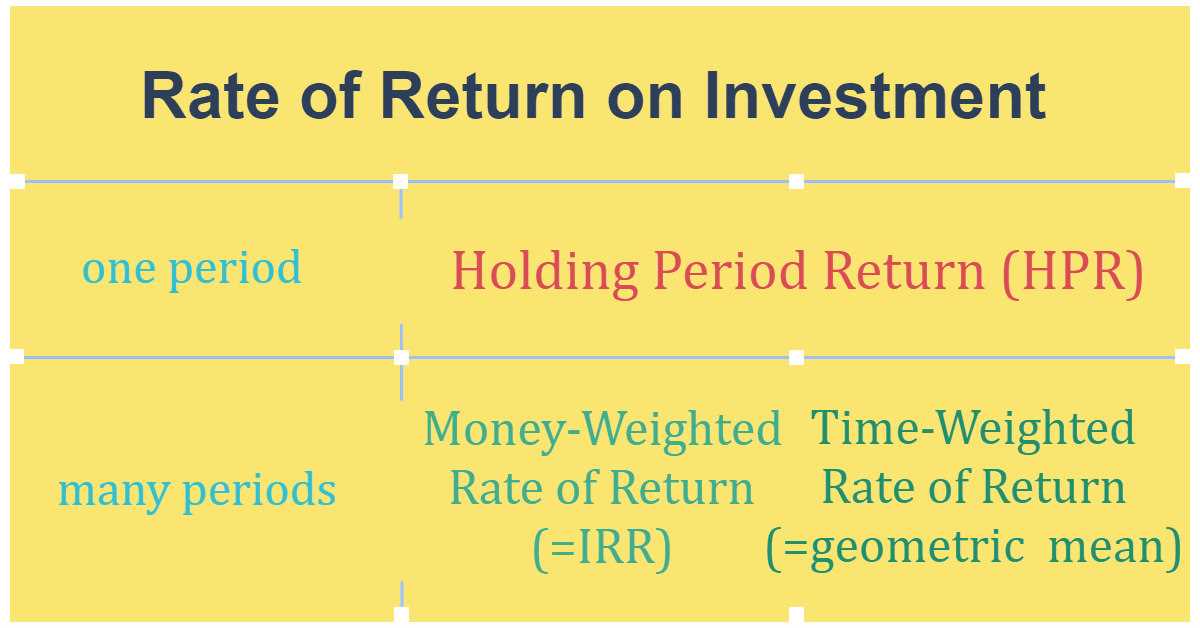
What is Money-Weighted Rate of Return?

Unlike the Time-Weighted Rate of Return, which focuses on the performance of the underlying investments, the Money-Weighted Rate of Return considers the impact of cash inflows and outflows on the overall return. This makes it a more accurate measure of the actual returns experienced by an investor.

Definition and Explanation

The Money-Weighted Rate of Return takes into account the timing and size of cash flows, which means that it reflects the impact of an investor’s buying and selling decisions. For example, if an investor adds a large sum of money to their portfolio during a period of high returns, the Money-Weighted Rate of Return will be higher compared to the Time-Weighted Rate of Return.

On the other hand, if an investor withdraws a significant amount of money during a period of low returns, the Money-Weighted Rate of Return will be lower compared to the Time-Weighted Rate of Return. This metric is particularly useful for evaluating the performance of investment portfolios with frequent cash flows, such as retirement accounts or mutual funds.

Money-Weighted Rate of Return Formula

The formula for calculating the Money-Weighted Rate of Return is:

Where:

• Ending Value of Portfolio is the value of the portfolio at the end of the measurement period.
• Beginning Value of Portfolio is the value of the portfolio at the beginning of the measurement period.
• Net Cash Flows is the difference between the cash inflows and outflows during the measurement period.

How to Calculate

Money-Weighted Rate of Return Example

Let’s say an investor starts with a portfolio value of $100,000. During the measurement period, they add $50,000 to their portfolio and the ending value of the portfolio is $150,000. The net cash flows would be $50,000 (positive because of the additional investment).

Using the formula, we can calculate the Money-Weighted Rate of Return:

Therefore, the Money-Weighted Rate of Return for this investment would be 150%.

Overall, the Money-Weighted Rate of Return provides a more accurate measure of an investor’s actual returns by considering the impact of cash flows. It is a useful metric for evaluating the performance of investment portfolios with frequent cash flows and can help investors make informed decisions about their investments.

Definition and Explanation

The money-weighted rate of return is a financial metric used to measure the performance of an investment portfolio. It takes into account the timing and amount of cash flows into and out of the portfolio, giving a more accurate representation of the investor’s actual return.

Unlike the time-weighted rate of return, which calculates the average return of the portfolio over a specific period of time, the money-weighted rate of return considers the impact of cash flows. This means that if an investor adds a large sum of money to the portfolio during a period of high returns, the money-weighted rate of return will reflect the higher returns achieved during that period.

The money-weighted rate of return is particularly useful for individual investors who regularly contribute or withdraw funds from their investment portfolios. It provides a more realistic measure of their investment performance, taking into account the impact of their cash flows.

To calculate the money-weighted rate of return, the cash flows into and out of the portfolio are weighted based on the timing and amount of each cash flow. The formula for calculating the money-weighted rate of return is:

By using this formula, investors can determine their actual rate of return, taking into account the impact of their cash flows. This can help them make more informed decisions about their investment strategies and evaluate the performance of their portfolios.

Money-Weighted Rate of Return Formula

The formula to calculate the money-weighted rate of return is as follows:

The money-weighted rate of return takes into account the timing and amount of cash flows, which means that it reflects the impact of any changes in investment amounts or withdrawals. This makes it a useful measure for investors who regularly contribute to or withdraw from their investment portfolios.

Overall, the money-weighted rate of return formula allows investors to evaluate the effectiveness of their investment decisions and determine the success of their investment strategy over a specific time period.

How to Calculate Money-Weighted Rate of Return

Calculating the money-weighted rate of return involves a few steps. Here’s how you can do it:

Step 1: Gather the necessary information

Before you can calculate the money-weighted rate of return, you need to gather some information. This includes the initial investment amount, any additional investments or withdrawals made during the investment period, and the ending value of the investment.

Step 2: Calculate the cash flows

Next, you need to calculate the cash flows for each period. This involves determining the amount of money invested or withdrawn during each period. If you made multiple investments or withdrawals, you will need to calculate the cash flows for each individual transaction.

Step 3: Calculate the time-weighted return for each period

Once you have the cash flows for each period, you can calculate the time-weighted return for each period. This is done by dividing the ending value of the investment by the beginning value and subtracting 1. Repeat this calculation for each period.

Step 4: Weight the returns by the cash flows

After calculating the time-weighted return for each period, you need to weight the returns by the cash flows. Multiply each time-weighted return by the corresponding cash flow to get the weighted return for each period.

Step 5: Sum the weighted returns

Finally, sum the weighted returns to get the total weighted return. This represents the money-weighted rate of return for the investment period.

Period	Cash Flow	Time-Weighted Return	Weighted Return
1	$10,000	0.05	$500
2	$5,000	0.03	$150
3	-$2,000	0.02	-$40
Total	$13,000		$610

Money-Weighted Rate of Return Example

Let’s consider an example to understand how to calculate the money-weighted rate of return. Suppose you invested $10,000 in a mutual fund at the beginning of the year. After six months, the value of your investment increased to $12,000. At this point, you decided to invest an additional $5,000 in the same fund.

After another six months, the value of your investment further increased to $18,000. At the end of the year, you decided to withdraw $3,000 from your investment. To calculate the money-weighted rate of return, we need to consider the timing and amount of each cash flow.

First, we calculate the return on the initial investment of $10,000. The return is the difference between the final value of $12,000 and the initial investment, which is $2,000. Next, we calculate the return on the additional investment of $5,000. The return is the difference between the final value of $18,000 and the additional investment, which is $13,000.

Now, we need to consider the timing and amount of the cash flows. The initial investment was made at the beginning of the year, so it was invested for the entire year. The additional investment was made after six months, so it was invested for the remaining six months of the year.

Therefore, the money-weighted rate of return for this investment is 100% ($15,000 / $15,000 * 100). This means that the investment generated a return equal to the total amount invested.

Illustration and Calculation

To better understand how the money-weighted rate of return is calculated, let’s consider an example.

Example:

Suppose you invest $10,000 in a mutual fund at the beginning of the year. After six months, the value of your investment has increased to $12,000. At this point, you decide to invest an additional $5,000 in the same fund. At the end of the year, the value of your investment has grown to $18,000.

First, we calculate the return on the initial investment. The return can be calculated using the formula:

Using the values from the example, the return on the initial investment is:

Next, we calculate the return on the additional investment. The return can be calculated using the same formula:

Using the values from the example, the return on the additional investment is:

Now, we need to calculate the weighted average return, taking into account the timing and amount of each cash flow.

To calculate the weighted average return, we use the formula:

Weighted Average Return = (Return on Initial Investment * Initial Investment + Return on Additional Investment * Additional Investment) / Total Investment

Using the values from the example, the weighted average return is:

Weighted Average Return = (0.2 * $10,000 + 2.6 * $5,000) / ($10,000 + $5,000) = 0.8 or 80%

Therefore, the money-weighted rate of return for this investment is 80%.

By calculating the money-weighted rate of return, investors can assess the performance of their investments, taking into account the timing and amount of each cash flow. It provides a more accurate measure of the actual return earned by the investor.