Annuity Due Definition
An annuity due is a type of financial arrangement in which a series of equal payments or cash flows are made at the beginning of each period, rather than at the end. In other words, it is an annuity in which the payment is made at the start of each period.
Annuities due are commonly used in various financial transactions, such as loans, leases, and insurance policies. They provide a steady stream of income or payments for a specified period of time.
Unlike ordinary annuities, where payments are made at the end of each period, annuities due have a slightly higher present value due to the time value of money. This is because the payments are received earlier, allowing for more time to earn interest or investment returns.
To calculate the present value of an annuity due, you can use the following formula:
| PV | = | PMT | * | / | r | |
| (1 + r) |
Where PV is the present value, PMT is the payment amount, r is the interest rate per period, and n is the number of periods.
Here are a few examples to illustrate annuity due:
Example 1: John invests $1,000 at an annual interest rate of 5% for 5 years, with payments made at the beginning of each year. The present value of the annuity due can be calculated using the formula mentioned above.
Example 2: Sarah leases a car and makes monthly payments of $300 at the beginning of each month for a period of 3 years. The present value of the annuity due can be calculated using the same formula.
Overall, annuities due offer flexibility and can be beneficial in certain financial situations. It is important to understand the concept and calculation of annuities due to make informed financial decisions.
What is an Annuity Due?

An annuity due is a type of financial arrangement in which a series of payments or cash flows are made at the beginning of each period, rather than at the end. It is essentially an ordinary annuity, but with payments made in advance.
Annuities due are commonly used in various financial situations, such as loan repayments, lease agreements, and retirement savings plans. They offer certain advantages over ordinary annuities, including a higher present value and a shorter duration.
Key Features of Annuity Due:
1. Payment Timing: In an annuity due, payments are made at the beginning of each period, which means the first payment is made immediately. This is in contrast to ordinary annuities, where payments are made at the end of each period.
2. Present Value: Due to the earlier payment timing, annuities due have a higher present value compared to ordinary annuities. This is because the cash flows received earlier have a higher value in terms of time value of money.
3. Duration: Annuities due have a shorter duration compared to ordinary annuities. This is because the payments are made earlier, resulting in a shorter period of cash flows.
Calculation Formula for Annuity Due:
The calculation formula for annuity due is similar to that of ordinary annuities, but with a slight modification. The formula is as follows:
| Variable | Definition |
|---|---|
| PMT | Payment amount |
| i | Interest rate per period |
| n | Number of periods |
| FV | Future value |
The formula for calculating the future value (FV) of an annuity due is:
Where:
PMT = Payment amount
i = Interest rate per period
n = Number of periods
Examples of Annuity Due:
1. A car lease agreement where the lessee makes monthly payments at the beginning of each month.
2. A mortgage loan where the borrower makes monthly payments at the beginning of each month.
3. An insurance policy where the policyholder makes annual premium payments at the beginning of each year.
Calculation Formula for Annuity Due
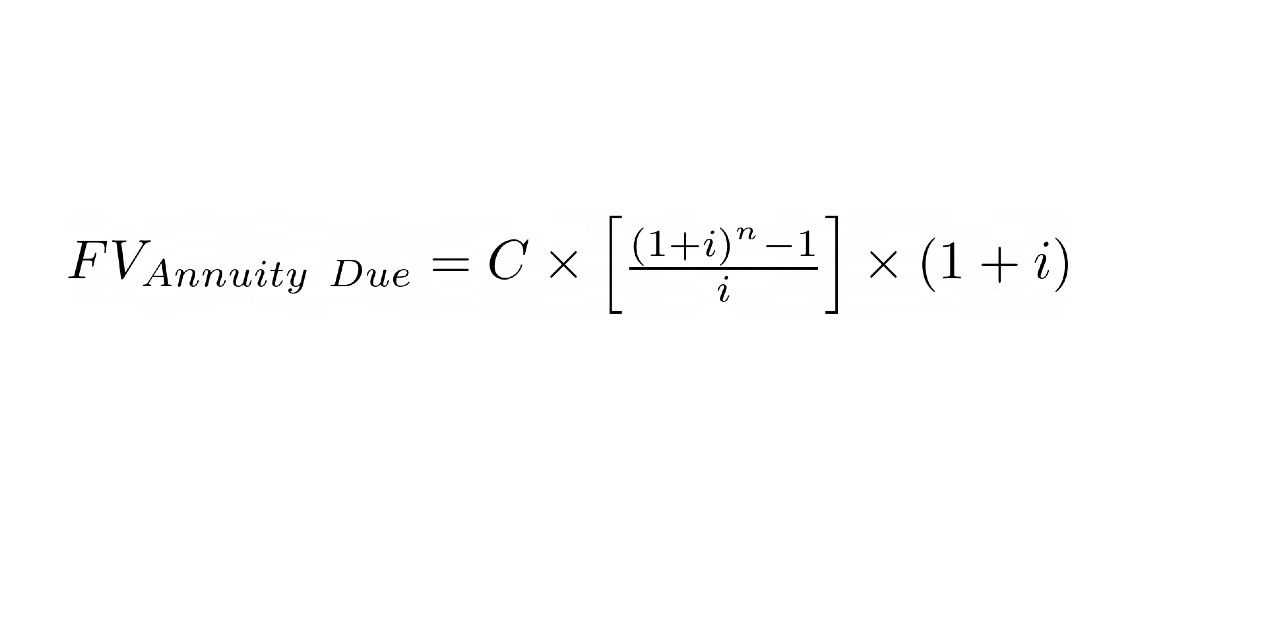
Annuity due refers to a series of equal cash flows or payments made at the beginning of each period. It is important to understand how to calculate the present value of an annuity due, as it can help in making financial decisions and analyzing investment opportunities.
The calculation formula for the present value of an annuity due is similar to that of a regular annuity, with one key difference. The formula is as follows:
Where:
- PV is the present value of the annuity due
- PMT is the amount of each payment or cash flow
- r is the interest rate per period
- n is the number of periods
The formula calculates the present value of the annuity due by discounting each cash flow back to its present value using the interest rate. The difference between an annuity due and a regular annuity is that the annuity due payments are made at the beginning of each period, so the formula adjusts for this by multiplying the entire expression by (1 + r).
By using this formula, you can determine the present value of an annuity due and make informed decisions about investments, loans, and other financial situations. It is important to note that the formula assumes a constant interest rate and equal cash flows throughout the annuity due.
Let’s consider an example to better understand the calculation formula for annuity due:
Example:
Suppose you want to calculate the present value of an annuity due with a payment of $1,000 made at the beginning of each year for a period of 5 years. The interest rate is 5% per year. Using the formula, we can calculate the present value as follows:
PV = $1,000 × [(-0.27628) / 0.05]
PV = $1,000 × (-5.5256)
PV = -$5,525.60
The present value of the annuity due is -$5,525.60. This negative value indicates that the annuity due is a liability or an outgoing cash flow.
Examples of Annuity Due
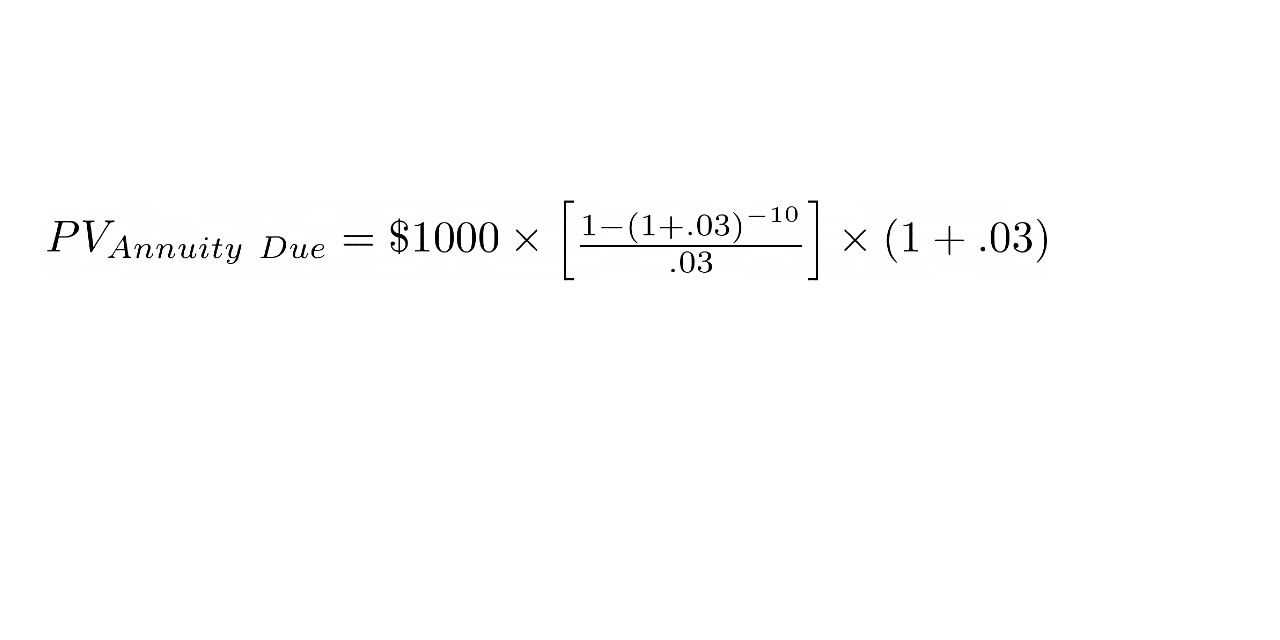
Here are some examples to help you understand annuity due:
-
Example 1:
Suppose you want to save money for your retirement by making monthly deposits into an annuity due. You decide to deposit $500 at the beginning of each month for a period of 20 years. The annuity due has an annual interest rate of 5%. To calculate the future value of the annuity, you can use the following formula:
Where:
- P is the monthly deposit amount ($500)
- r is the monthly interest rate (5% / 12 = 0.4167%)
- n is the number of months (20 years * 12 months = 240)
By plugging in the values into the formula, you can calculate that the future value of the annuity will be approximately $193,219.83.
-
Example 2:
Let’s say you win a lottery and receive a lump sum payment of $1,000,000. You decide to invest this money into an annuity due with an annual interest rate of 6% for a period of 30 years. The annuity due pays out monthly. To calculate the monthly payment amount, you can use the following formula:
Where:
- PV is the present value of the annuity ($1,000,000)
- r is the monthly interest rate (6% / 12 = 0.5%)
- n is the number of months (30 years * 12 months = 360)
By plugging in the values into the formula, you can calculate that the monthly payment amount will be approximately $5,995.49.
These examples demonstrate how annuity due can be used to save for retirement or receive regular income from a lump sum payment. It is important to consider the interest rate, deposit/payment amounts, and the duration of the annuity when making financial decisions.

Emily Bibb simplifies finance through bestselling books and articles, bridging complex concepts for everyday understanding. Engaging audiences via social media, she shares insights for financial success. Active in seminars and philanthropy, Bibb aims to create a more financially informed society, driven by her passion for empowering others.
