Effective Annual Interest Rate Definition Formula and Example

What is Effective Annual Interest Rate?

Definition of Effective Annual Interest Rate

The effective annual interest rate is the annualized interest rate that takes into account the effect of compounding. It represents the true cost or return on an investment or loan over a one-year period. By considering the compounding of interest, the effective annual interest rate provides a more accurate measure of the actual cost or return compared to the nominal interest rate.

The effective annual interest rate is particularly useful when comparing different financial products, such as savings accounts, loans, or credit cards. It allows individuals to determine which option will provide the highest return on investment or the lowest cost of borrowing.

Formula for Calculating Effective Annual Interest Rate

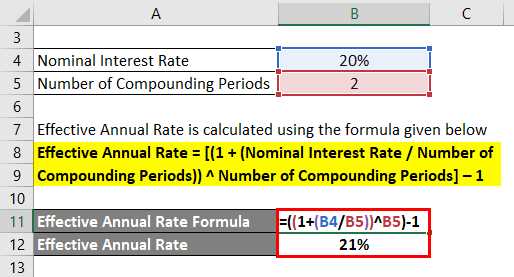
The formula for calculating the effective annual interest rate is:

Where:

• AER is the effective annual interest rate
• r is the nominal interest rate
• n is the number of compounding periods per year

By plugging in the values for the nominal interest rate and the number of compounding periods, individuals can calculate the effective annual interest rate for a given financial product.

Example of Effective Annual Interest Rate Calculation

Let’s say you are considering two savings accounts. Account A offers a nominal interest rate of 5% compounded annually, while Account B offers a nominal interest rate of 4.8% compounded quarterly.

Using the formula for calculating the effective annual interest rate, we can determine the true cost or return of each account:

For Account A:

AER = 0.05 or 5%

For Account B:

AER = 0.049 or 4.9%

Based on the calculations, Account A has an effective annual interest rate of 5%, while Account B has an effective annual interest rate of 4.9%. Therefore, Account A would provide a higher return on investment compared to Account B.

Overall, the effective annual interest rate is a valuable tool for individuals to make informed financial decisions. It allows them to compare different financial products and determine the true cost or return, taking into account the compounding of interest.

Definition of Effective Annual Interest Rate

The effective annual interest rate is a crucial concept in finance as it allows investors and borrowers to compare different financial products and determine which one offers the best return or cost. It provides a standardized way of comparing interest rates that may have different compounding periods or terms.

Unlike the nominal interest rate, which is the stated interest rate without considering compounding, the effective annual interest rate reflects the impact of compounding on the overall return or cost. It takes into account the frequency of compounding, such as annually, semi-annually, quarterly, or monthly, and calculates the equivalent annual rate that would produce the same result.

The formula for calculating the effective annual interest rate is:

Where:

• EAR is the effective annual interest rate
• i is the nominal interest rate
• n is the number of compounding periods per year

For example, if a bank offers a nominal interest rate of 5% compounded semi-annually, the effective annual interest rate would be:

Formula for Calculating Effective Annual Interest Rate

The effective annual interest rate is a measure of the true annual interest rate that takes into account the effects of compounding. It is often used to compare different investment options or loans to determine which one offers the best return or lowest cost.

The formula for calculating the effective annual interest rate is:

Where:

• The Nominal Interest Rate is the stated annual interest rate, usually expressed as a percentage.
• The Number of Compounding Periods is the number of times that interest is compounded per year.

To calculate the effective annual interest rate, you need to know the nominal interest rate and the number of compounding periods. The formula takes into account the compounding effect by raising the sum of 1 and the nominal interest rate divided by the number of compounding periods to the power of the number of compounding periods, and then subtracting 1.

For example, let’s say you have a nominal interest rate of 5% and interest is compounded annually. Using the formula, the effective annual interest rate would be:

= 0.05 or 5%

However, if the interest is compounded more frequently, such as quarterly or monthly, the effective annual interest rate will be higher than the nominal interest rate. This is because the compounding effect increases the overall return or cost of the investment or loan.

By using the formula for calculating the effective annual interest rate, investors and borrowers can make more informed decisions about their financial options and understand the true cost or return of their investments or loans.

Example of Effective Annual Interest Rate Calculation

Let’s say you are considering two different investment options: Option A offers an annual interest rate of 5% compounded semi-annually, while Option B offers an annual interest rate of 4.8% compounded quarterly. To determine which option will give you a higher effective annual interest rate, you can use the formula for calculating the effective annual interest rate.

First, let’s calculate the effective annual interest rate for Option A:

1. Add 1 to the result from step 1. 1 + 0.025 equals 1.025.
2. Multiply the result from step 4 by 100 to convert it to a percentage. 0.050625 multiplied by 100 equals 5.0625%.

Therefore, the effective annual interest rate for Option A is 5.0625%.

Now, let’s calculate the effective annual interest rate for Option B:

1. Add 1 to the result from step 1. 1 + 0.012 equals 1.012.
2. Multiply the result from step 4 by 100 to convert it to a percentage. 0.048096 multiplied by 100 equals 4.8096%.

Therefore, the effective annual interest rate for Option B is 4.8096%.

Based on the calculations, Option A has a higher effective annual interest rate of 5.0625% compared to Option B’s 4.8096%. This means that Option A will yield a higher return on investment over the course of a year.

It is important to calculate the effective annual interest rate when comparing different investment options, as it provides a more accurate measure of the true return on investment.