Addition Rule for Probabilities Formula and What It Tells You

Addition Rule for Probabilities Formula and What It Tells You

The addition rule for probabilities is a fundamental concept in probability theory that allows us to calculate the probability of the union of two or more events. It is based on the principle that the probability of the union of two events is equal to the sum of their individual probabilities minus the probability of their intersection.

Formula

The formula for the addition rule for probabilities is:

Where:

• P(A or B) represents the probability of event A or event B occurring
• P(A) represents the probability of event A occurring
• P(B) represents the probability of event B occurring
• P(A and B) represents the probability of both event A and event B occurring

This formula allows us to calculate the probability of the union of two events, taking into account the probability of their intersection. By subtracting the probability of their intersection, we avoid double-counting the overlapping portion.

What It Tells You

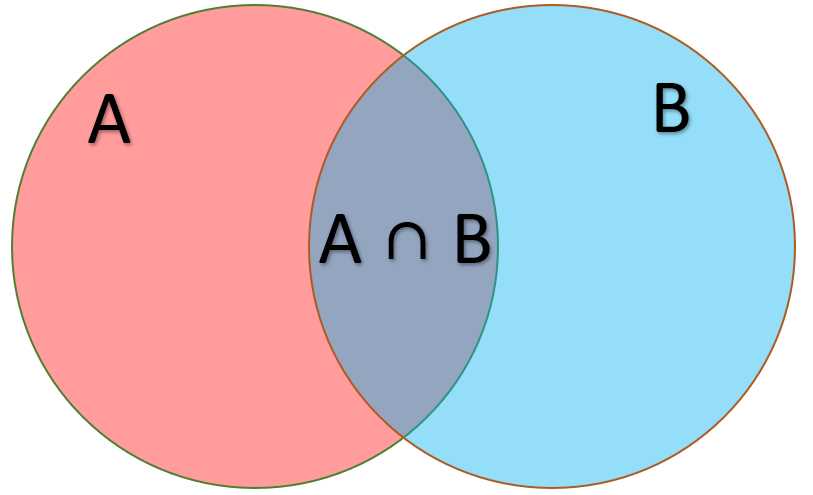
The addition rule for probabilities tells us how to calculate the probability of the union of two events. It provides a way to combine the individual probabilities of events to determine the overall probability of their occurrence. By considering the probability of their intersection, it accounts for the overlap between the events.

By using the addition rule for probabilities, we can analyze real-life scenarios and calculate the probability of different combinations of events. This can be particularly useful in situations where multiple events can occur simultaneously or where the occurrence of one event affects the probability of another event.

Overall, the addition rule for probabilities is a powerful tool in probability theory that enables us to calculate the probability of the union of events and make informed decisions based on the likelihood of different outcomes.

The Addition Rule for Probabilities is a fundamental concept in probability theory that allows us to calculate the probability of the union of two or more events. It states that the probability of the union of two events A and B is equal to the sum of their individual probabilities minus the probability of their intersection.

Formula

The formula for the Addition Rule for Probabilities is:

Where:

• P(A ∪ B) is the probability of the union of events A and B
• P(A) is the probability of event A
• P(B) is the probability of event B
• P(A ∩ B) is the probability of the intersection of events A and B

This formula allows us to calculate the probability of the union of two events by considering their individual probabilities and the probability of their intersection. By subtracting the probability of the intersection, we avoid double-counting the overlapping region.

For example, in finance, the Addition Rule for Probabilities can be used to calculate the probability of a stock price either increasing or decreasing based on different market conditions. In risk analysis, it can help assess the probability of multiple risks converging and causing a significant impact on a project or business.

It is important to note that the Addition Rule for Probabilities assumes that the events are mutually exclusive or independent. If the events are dependent, the formula may need to be modified accordingly.

Applying the Addition Rule for Probabilities in Real-Life Scenarios

The Addition Rule for Probabilities is a fundamental concept in probability theory that allows us to calculate the probability of the union of two or more events. This rule is widely applicable in various real-life scenarios where we need to determine the likelihood of multiple events occurring simultaneously or independently.

One practical example where the Addition Rule for Probabilities can be applied is in the field of finance. Let’s say you are an investor and you are considering investing in two different stocks. You want to calculate the probability of both stocks performing well in a given year.

First, you need to determine the individual probabilities of each stock performing well. Let’s assume that the probability of Stock A performing well is 0.6, and the probability of Stock B performing well is 0.7. According to the Addition Rule for Probabilities, the probability of both stocks performing well is the sum of their individual probabilities, which is 0.6 + 0.7 = 1.3.

Another real-life scenario where the Addition Rule for Probabilities can be applied is in the field of weather forecasting. Let’s say you want to determine the probability of it raining or snowing on a particular day. You have historical data that shows the probability of rain is 0.4, and the probability of snow is 0.3.

Using the Addition Rule for Probabilities, you can calculate the probability of either rain or snow by adding their individual probabilities, which is 0.4 + 0.3 = 0.7. This means that there is a 70% chance of either rain or snow occurring on that day.