Importance of Greeks in Options and Derivatives
The Greeks provide insights into how the price of an option or derivative is affected by various factors, such as changes in the underlying asset price, time decay, volatility, and interest rates. By analyzing the Greeks, traders and investors can make informed decisions about their positions and effectively manage their risk exposure.
One of the most important Greeks is Delta. Delta measures the sensitivity of an option’s price to changes in the price of the underlying asset. It indicates how much the option’s price will change for a one-point increase or decrease in the underlying asset price. Delta helps traders assess the directional risk of their options positions and hedge against adverse price movements.
Vega is the Greek that measures the sensitivity of an option’s price to changes in volatility. It indicates how much the option’s price will change for a one-percentage-point increase or decrease in volatility. Vega is crucial for options traders as it helps them assess the impact of changes in market volatility on their positions and adjust their strategies accordingly.
Rho measures the sensitivity of an option’s price to changes in interest rates. It indicates how much the option’s price will change for a one-percentage-point increase or decrease in interest rates. Rho is particularly important for options traders when interest rates are expected to change significantly, as it helps them assess the impact of interest rate movements on their positions.
Common Greeks Used in Finance
Delta
Delta measures the sensitivity of the option price to changes in the price of the underlying asset. It indicates how much the option price will change for a one-point movement in the underlying asset. A delta of 0.5 means that for every one-point increase in the underlying asset, the option price will increase by 0.5 points.
Gamma

Gamma measures the rate of change of delta. It shows how much the delta will change for a one-point movement in the underlying asset. Gamma is important for traders who want to adjust their positions to maintain a desired level of delta exposure.
Theta
Theta measures the time decay of an option. It shows how much the option price will decrease as time passes. Theta is particularly important for options traders who want to understand the impact of time on the value of their positions.
Vega
Vega measures the sensitivity of the option price to changes in volatility. It indicates how much the option price will change for a one-point increase in volatility. Vega is crucial for traders who want to assess the impact of changes in market volatility on their options positions.
These are just a few of the common Greeks used in finance. Other Greeks include Rho, which measures the sensitivity of the option price to changes in interest rates, and Charm, which measures the rate of change of delta with respect to time.
Calculating and Interpreting Greeks
There are several common Greeks used in finance:
| Greek | Definition |
|---|---|
| Delta | Measures the change in option price for a $1 change in the underlying asset price. |
| Gamma | Measures the rate of change of delta for a $1 change in the underlying asset price. |
| Theta | Measures the change in option price for a 1-day decrease in time to expiration. |
| Vega | Measures the change in option price for a 1% increase in volatility. |
| Rho | Measures the change in option price for a 1% increase in interest rates. |
Managing Risk with Greeks in Finance
What are Greeks in Finance?
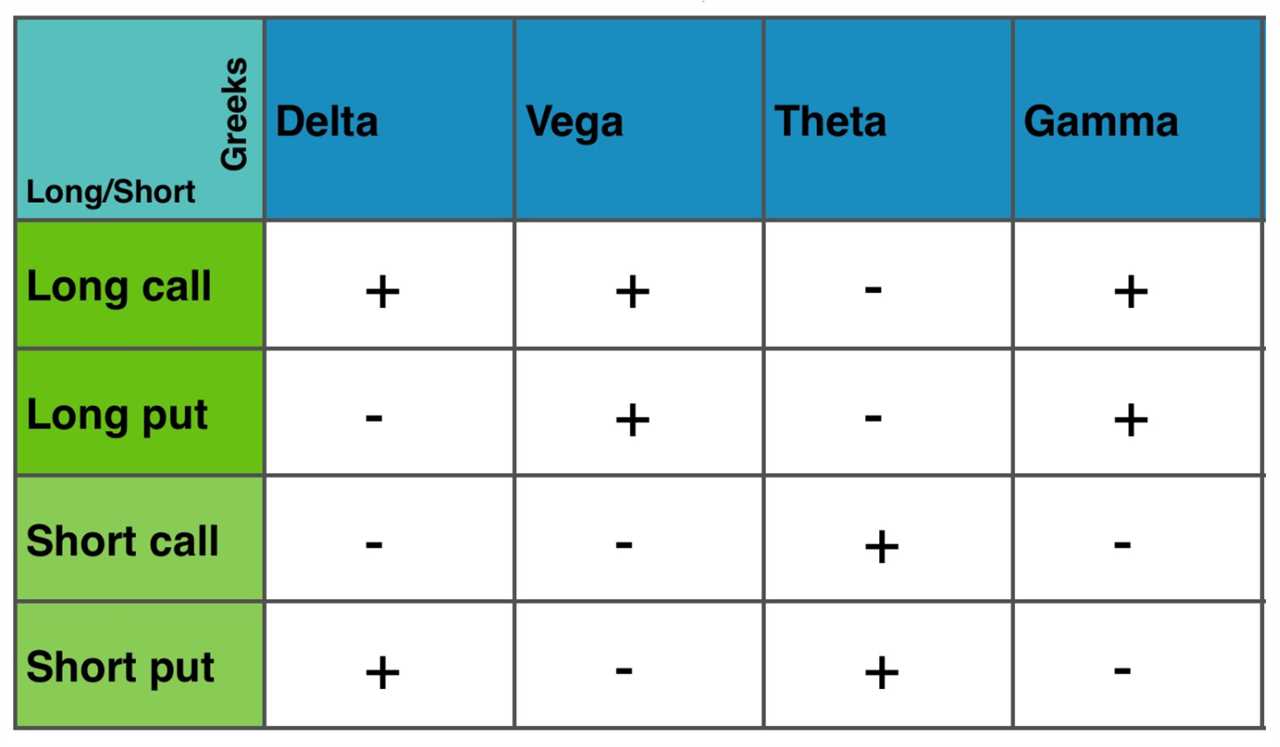
Greeks in finance are mathematical calculations that quantify the sensitivity of options and derivatives to various factors such as price changes, time decay, volatility, and interest rates. These calculations provide valuable insights into the potential risks and rewards of a particular position.
Types of Greeks
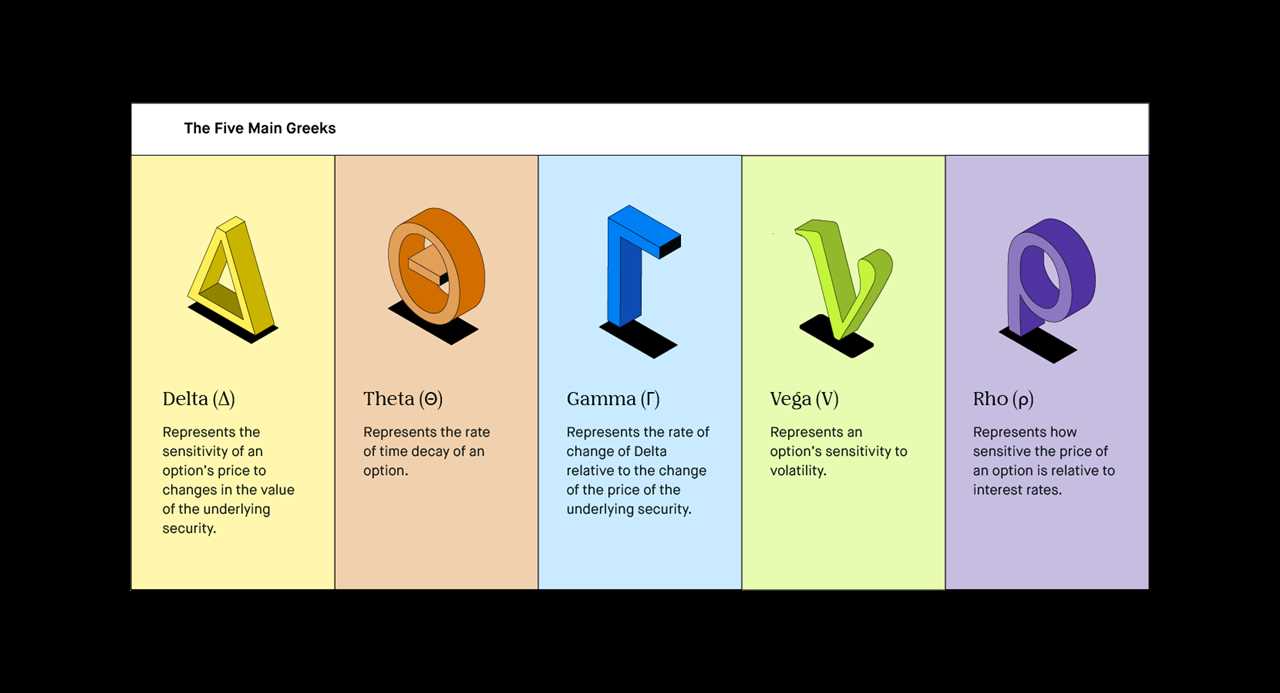
There are several common Greeks used in finance, including:
- Delta: Measures the change in the option price relative to a change in the underlying asset price.
- Gamma: Measures the rate of change of delta.
- Theta: Measures the impact of time decay on the option price.
- Vega: Measures the sensitivity of the option price to changes in volatility.
- Rho: Measures the sensitivity of the option price to changes in interest rates.
Calculating and Interpreting Greeks
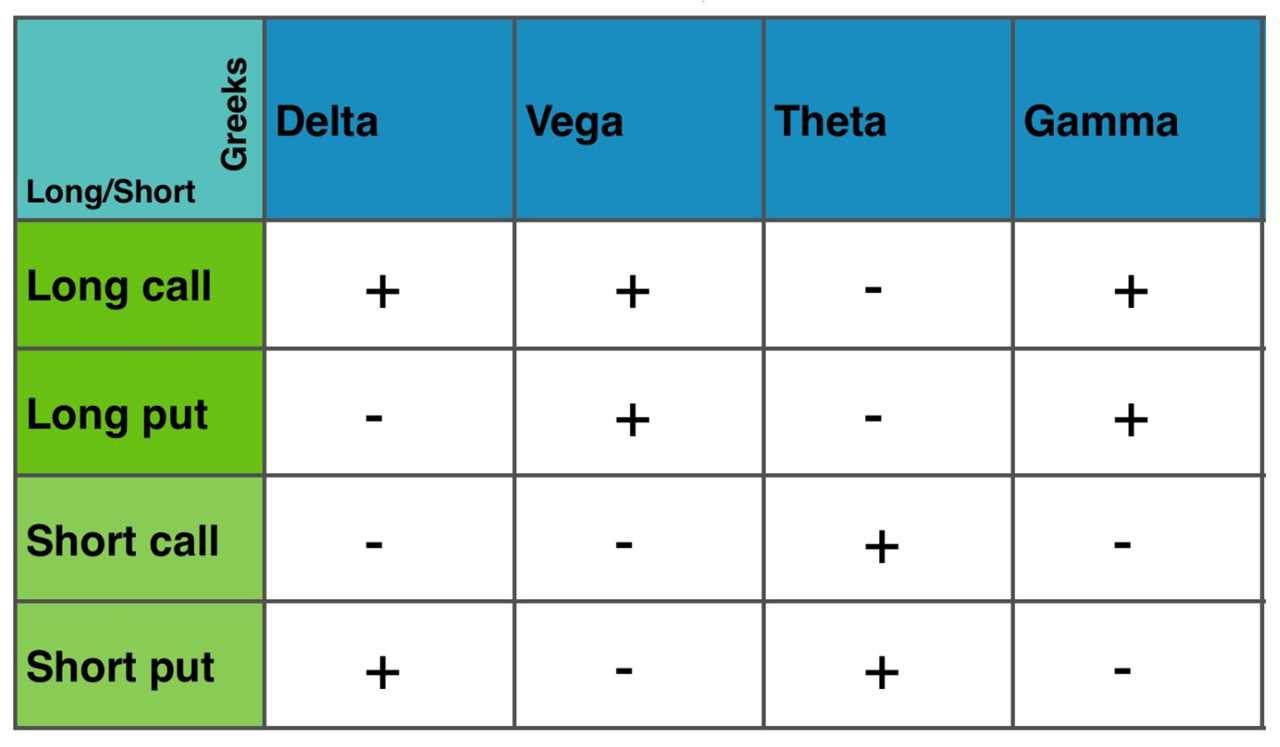
To calculate the Greeks, traders use complex mathematical models and option pricing formulas. These calculations provide valuable information about the potential risks and rewards of a particular position.
Interpreting the Greeks is equally important. Traders can use the Greeks to assess the impact of different scenarios on their positions. For example, delta can help determine the likelihood of an option expiring in-the-money, while theta can indicate the rate at which an option loses value over time.
Managing Risk with Greeks
For example, if a trader wants to hedge against a potential drop in the underlying asset price, they can use delta to determine the appropriate number of options to buy or sell to offset the risk. Similarly, vega can help traders adjust their positions to account for changes in volatility.
Overall, managing risk with Greeks in finance is essential for successful options and derivatives trading. By utilizing the insights provided by the Greeks, traders can make more informed decisions and protect themselves against potential losses.

Emily Bibb simplifies finance through bestselling books and articles, bridging complex concepts for everyday understanding. Engaging audiences via social media, she shares insights for financial success. Active in seminars and philanthropy, Bibb aims to create a more financially informed society, driven by her passion for empowering others.
