Perpetuity Financial Definition Formula and Examples

Perpetuity Financial Definition

A perpetuity is a type of financial instrument that provides a stream of cash flows that continues indefinitely. It is a form of annuity that has no end date, meaning the payments will continue forever. Perpetuities are commonly used in finance and investment to value assets and determine their present worth.

Formula for Perpetuity

The formula for calculating the present value of a perpetuity is:

PV = C / r

Where PV is the present value, C is the cash flow received each period, and r is the discount rate or the required rate of return.

Example of Perpetuity

Let’s say you have invested in a perpetuity that pays $1,000 every year. If the discount rate is 5%, you can calculate the present value of the perpetuity using the formula:

PV = $1,000 / 0.05 = $20,000

This means that the present value of the perpetuity is $20,000. In other words, if you were to receive $1,000 every year indefinitely and the discount rate is 5%, the present value of those cash flows would be $20,000.

Perpetuities are commonly used in the valuation of stocks, bonds, and other financial instruments. They are also used to determine the value of real estate properties that generate rental income.

What is Perpetuity?

A perpetuity is a financial concept that refers to a stream of cash flows that continues indefinitely. It is a type of annuity that has no end date, meaning it pays out a fixed amount of money at regular intervals forever. Perpetuities are often used in finance and investment calculations to determine the present value of a never-ending cash flow.

In simple terms, a perpetuity is like a never-ending income stream. It is a financial instrument that promises to pay a fixed amount of money at regular intervals, such as annually or monthly, without ever terminating. This makes perpetuities different from other types of annuities, which have a specific end date or time period.

The concept of perpetuity is commonly used in various financial calculations, such as valuing bonds, stocks, and real estate. It helps investors and analysts determine the present value of an investment or cash flow that is expected to continue indefinitely. By calculating the present value of a perpetuity, investors can assess the worth of an investment and make informed decisions.

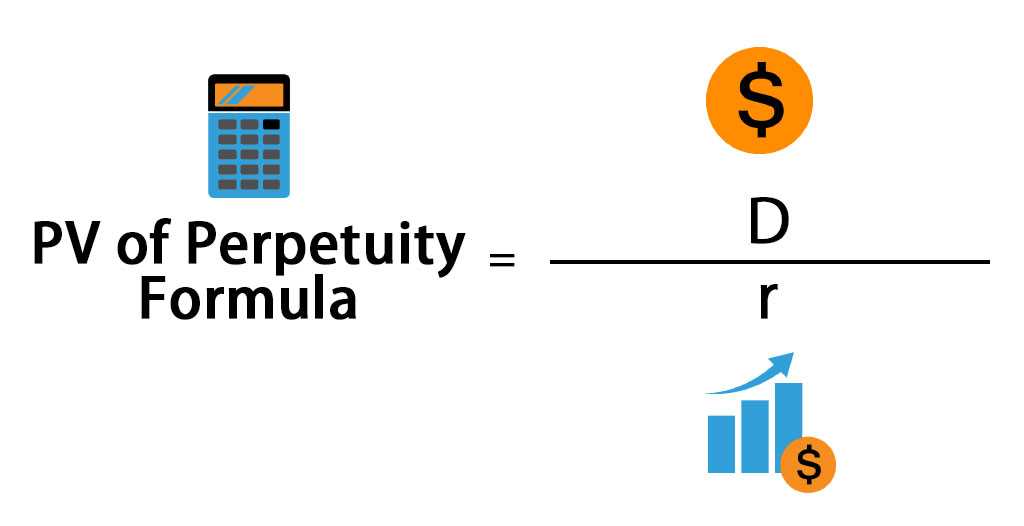
The formula for calculating the present value of a perpetuity is:

PV = C / r

Where PV is the present value, C is the cash flow, and r is the discount rate or the required rate of return. The discount rate represents the opportunity cost of investing in the perpetuity, and it is used to determine the present value of the cash flows.

For example, let’s say you have an investment that promises to pay $1,000 annually forever, and the required rate of return is 5%. Using the perpetuity formula, the present value of this perpetuity would be:

PV = $1,000 / 0.05 = $20,000

Perpetuity Formula

A perpetuity is a type of financial arrangement that involves a series of equal payments that continue indefinitely. The perpetuity formula is used to calculate the present value of these future cash flows. The formula for calculating the present value of a perpetuity is:

PV = C / r

Where:

• PV is the present value of the perpetuity
• C is the cash flow received each period
• r is the discount rate or the required rate of return

The perpetuity formula assumes that the cash flows will continue indefinitely and that the discount rate remains constant. It is important to note that the discount rate should be greater than the growth rate of the cash flows in order for the perpetuity formula to be applicable.

Example:

Let’s say you are considering investing in a perpetuity that pays $1,000 per year. You require a 5% return on your investment. Using the perpetuity formula, you can calculate the present value of the perpetuity as follows:

PV = $1,000 / 0.05 = $20,000

Therefore, the present value of the perpetuity is $20,000. This means that if you invest $20,000 today, you can expect to receive $1,000 per year indefinitely, assuming a 5% return on your investment.

Perpetuity Examples

In finance, a perpetuity is a stream of cash flows that continues indefinitely. It is a type of annuity that has no end date. Perpetuities are often used in financial calculations to determine the present value of a cash flow that is expected to continue indefinitely.

Here are a few examples of perpetuities:

1. Dividend Perpetuity:

2. Bond Perpetuity:

A bond that has no maturity date and pays a fixed coupon indefinitely is an example of a bond perpetuity. These types of bonds are rare, but they do exist. Investors can calculate the present value of the future coupon payments using the perpetuity formula.

3. Real Estate Perpetuity:

Investors who own rental properties can receive rental income indefinitely, making it a perpetuity. The present value of the future rental income can be calculated using the perpetuity formula.

It is important to note that perpetuities are theoretical concepts and may not always exist in reality. However, they can be useful in financial modeling and valuation to estimate the value of cash flows that are expected to continue indefinitely.

Annuities catname

Annuities catname refers to a specific category of annuities that are designed to provide a fixed income stream for the lifetime of the annuitant. An annuity is a financial product that is typically purchased from an insurance company and provides regular payments to the annuitant in exchange for a lump sum or a series of payments.

Unlike other types of annuities, annuities catname are structured as perpetuities, which means that they are designed to provide payments for an indefinite period of time. This is in contrast to annuities with a fixed term, which provide payments for a specific number of years.

One of the key advantages of annuities catname is that they offer the potential for a guaranteed income stream for life, regardless of market conditions. This can provide peace of mind for individuals who are concerned about outliving their savings or who want to ensure a stable income during retirement.