Bond Valuation Calculation
Bond valuation is a method used to determine the fair value of a bond. It involves calculating the present value of the bond’s future cash flows, including both interest payments and the return of principal at maturity. This calculation is important for investors and analysts to assess the attractiveness of a bond investment.
Definition of Bond Valuation
Bond valuation is the process of determining the intrinsic value of a bond. It takes into account the bond’s coupon rate, maturity date, and market interest rates to calculate the present value of its cash flows. The present value is then compared to the bond’s market price to assess whether it is overvalued or undervalued.
Formula for Bond Valuation
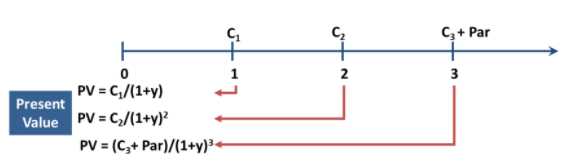
The formula for bond valuation is as follows:
| PV = C1/(1+r)^1 + C2/(1+r)^2 + … + Cn/(1+r)^n + F/(1+r)^n |
Where:
- PV is the present value of the bond
- C1, C2, …, Cn are the cash flows (interest payments) received at each period
- F is the principal amount (face value) received at maturity
- r is the discount rate or required rate of return
- n is the number of periods until maturity
The discount rate used in the formula is typically the market interest rate for bonds with similar characteristics.
Example of Bond Valuation
Let’s consider an example to illustrate the bond valuation calculation. Suppose we have a bond with a face value of $1,000, a coupon rate of 5%, and a maturity of 5 years. The market interest rate for similar bonds is 4%. The bond pays interest semi-annually.
To calculate the present value of the bond, we need to discount the cash flows at the market interest rate. The cash flows consist of 10 semi-annual interest payments of $25 each and the principal amount of $1,000 received at maturity.
Using the bond valuation formula, we can calculate the present value as follows:
| PV = $25/(1+0.04/2)^1 + $25/(1+0.04/2)^2 + … + $25/(1+0.04/2)^10 + $1,000/(1+0.04/2)^10 |
By calculating the above expression, we find that the present value of the bond is approximately $1,037.47. Therefore, if the market price of the bond is lower than $1,037.47, it would be considered undervalued, and if it is higher, it would be considered overvalued.
Overall, bond valuation calculation is a crucial tool for investors to determine the fair value of a bond and make informed investment decisions.
Definition of Bond Valuation
Bond valuation is the process of determining the fair value of a bond, which represents the present value of the bond’s future cash flows. It is an essential concept in finance and investment analysis, as it helps investors and analysts evaluate the attractiveness of a bond investment.
When a company or government issues a bond, it promises to make periodic interest payments to the bondholders and repay the principal amount at maturity. The value of a bond is determined by discounting these future cash flows back to their present value using an appropriate discount rate.
Factors Affecting Bond Valuation
Several factors influence the valuation of a bond:
- Credit Rating: The creditworthiness of the issuer, as reflected in its credit rating, influences bond valuation. Bonds issued by entities with higher credit ratings are considered less risky and, therefore, more valuable.
Bond Valuation Formula
The formula for bond valuation is:
| Value of Bond | = | + | (Face Value / (1 + Discount Rate)^Number of Periods) |
Where:
- Coupon Payment: The periodic interest payment made by the bond.
- Discount Rate: The required rate of return or discount rate used to discount the bond’s future cash flows.
- Number of Periods: The total number of periods until the bond’s maturity.
- Face Value: The principal amount of the bond to be repaid at maturity.
Example of Bond Valuation
Let’s consider an example to illustrate bond valuation. Assume a bond with a face value of $1,000, a coupon rate of 5% paid annually, a discount rate of 6%, and a maturity of 5 years. Using the bond valuation formula, we can calculate the value of the bond as follows:
| Coupon Payment | = | $1,000 * 5% | = | $50 |
| Discount Rate | = | 6% | ||
| Number of Periods | = | 5 years | ||
| Face Value | = | $1,000 |
Using the formula:
| Value of Bond | = | + | ($1,000 / (1 + 6%)^5) | |
| Value of Bond | = | $437.60 | + | $747.26 |
| Value of Bond | = | $1,184.86 |
Therefore, the value of the bond is $1,184.86.
Formula for Bond Valuation
Bond valuation is the process of determining the fair value of a bond. It involves calculating the present value of the bond’s future cash flows, including both the periodic interest payments and the principal repayment at maturity. The formula for bond valuation is as follows:
Present Value of Interest Payments

The present value of the bond’s interest payments is calculated using the formula:
Present Value of Interest Payments = (Coupon Payment / (1 + Yield to Maturity)^1) + (Coupon Payment / (1 + Yield to Maturity)^2) + … + (Coupon Payment / (1 + Yield to Maturity)^n)
Where:
- Coupon Payment is the periodic interest payment made by the bond
- Yield to Maturity is the required rate of return on the bond
- n is the number of periods until the bond matures
Present Value of Principal Repayment
The present value of the bond’s principal repayment at maturity is calculated using the formula:
Present Value of Principal Repayment = Principal / (1 + Yield to Maturity)^n
Where:
- Principal is the face value or par value of the bond
- Yield to Maturity is the required rate of return on the bond
- n is the number of periods until the bond matures
Total Bond Valuation
The total bond valuation is calculated by summing the present value of the bond’s interest payments and the present value of the principal repayment:
Total Bond Valuation = Present Value of Interest Payments + Present Value of Principal Repayment
This formula allows investors to determine the fair value of a bond based on its cash flows and the required rate of return. By comparing the calculated bond valuation to the market price of the bond, investors can assess whether the bond is overvalued or undervalued.
Example of Bond Valuation

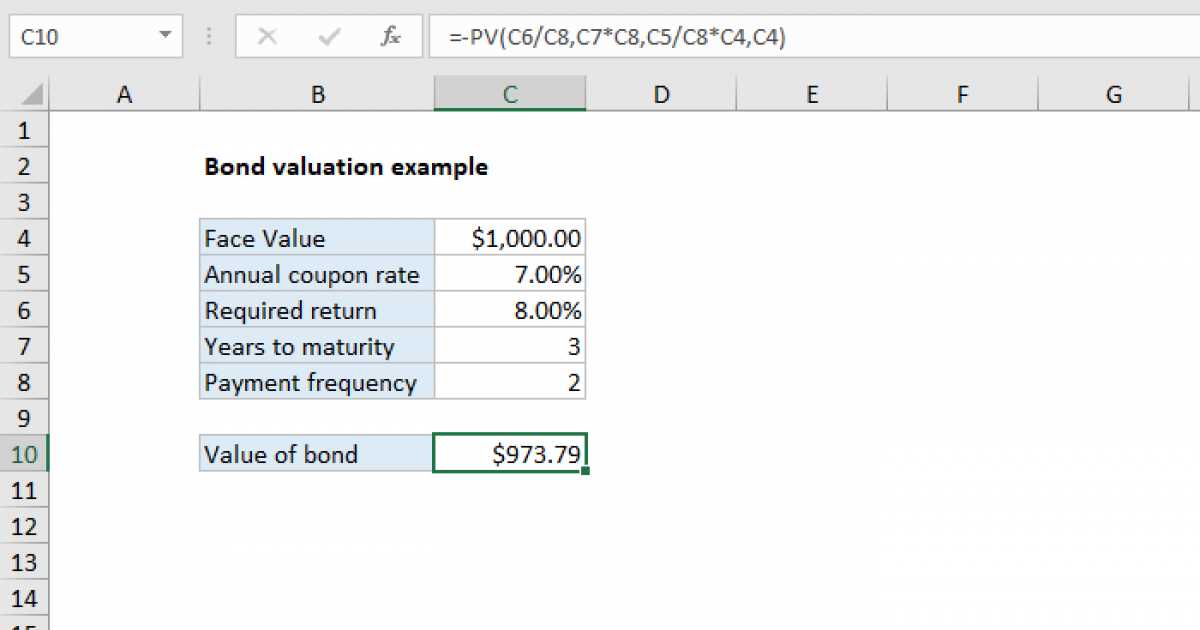
Let’s consider an example to understand the concept of bond valuation. Suppose there is a company named XYZ Ltd. that issued a bond with a face value of $1,000 and a coupon rate of 5%. The bond has a maturity period of 5 years.
To calculate the present value of the bond, we need to discount the future cash flows generated by the bond. The cash flows consist of periodic coupon payments and the final principal repayment at maturity.
Next, we need to discount these coupon payments to their present value. The discount rate used for discounting is usually the required rate of return or the yield to maturity. Let’s assume the discount rate is 6%.
Using the formula for present value of a bond, we can calculate the present value of the coupon payments as follows:
PV of coupon payments = $50 / (1 + 6%)^1 + $50 / (1 + 6%)^2 + $50 / (1 + 6%)^3 + $50 / (1 + 6%)^4 + $50 / (1 + 6%)^5 = $46.98 + $44.28 + $41.86 + $39.70 + $37.78 = $210.60
Finally, we need to calculate the present value of the principal repayment at maturity. Since the face value of the bond is $1,000 and the discount rate is 6%, we can calculate the present value of the principal repayment as follows:
PV of principal repayment = $1,000 / (1 + 6%)^5 = $747.26
Now, we can calculate the total present value of the bond by summing up the present value of the coupon payments and the present value of the principal repayment:
Total present value of the bond = $210.60 + $747.26 = $957.86

Emily Bibb simplifies finance through bestselling books and articles, bridging complex concepts for everyday understanding. Engaging audiences via social media, she shares insights for financial success. Active in seminars and philanthropy, Bibb aims to create a more financially informed society, driven by her passion for empowering others.
