P-Value Calculation and Significance: A Comprehensive Guide

P-Value Calculation and Significance: A Comprehensive Guide

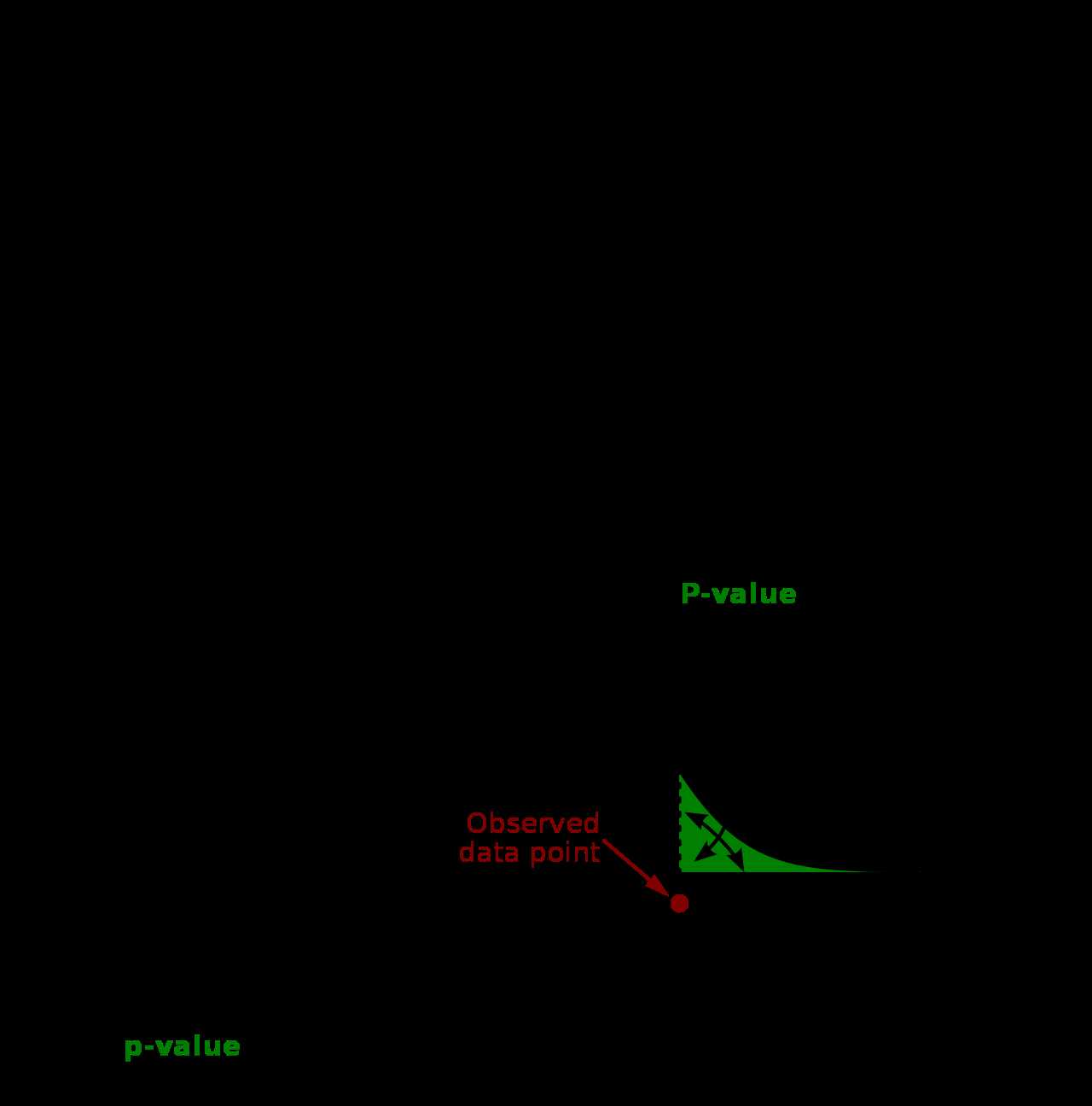
To calculate the p-value, one must first define the null hypothesis and alternative hypothesis. The null hypothesis represents the absence of any significant effect or relationship, while the alternative hypothesis suggests the presence of such an effect. The p-value is then calculated based on the observed data and the assumed distribution under the null hypothesis.

There are various statistical tests that can be used to calculate the p-value, depending on the type of data and the research question. Some commonly used tests include t-tests, chi-square tests, and analysis of variance (ANOVA). Each test has its own assumptions and requirements, and it is important to choose the appropriate test for the specific analysis.

Once the p-value is calculated, it is compared to a predetermined significance level, typically denoted as alpha (α). The significance level represents the threshold for determining whether the results are statistically significant. If the p-value is less than the significance level, it is considered statistically significant, indicating that the null hypothesis can be rejected in favor of the alternative hypothesis.

Interpreting the p-value results requires careful consideration of the context and the specific research question. It is important to note that statistical significance does not necessarily imply practical significance. A statistically significant result may have little practical importance, while a non-significant result may still be meaningful in certain contexts.

When interpreting p-values, it is also important to consider the limitations and potential sources of error. Common mistakes in p-value calculation include using incorrect formulas, failing to account for multiple comparisons, and misinterpreting the results. It is crucial to double-check calculations and seek expert advice when necessary to ensure accurate and reliable results.

Advanced techniques for p-value calculation and significance testing are constantly evolving in the field of finance. Researchers and analysts are continually developing new methods and approaches to improve the accuracy and reliability of p-value calculations. Staying updated with the latest advancements in statistical analysis can help enhance the quality of financial analysis and decision-making.

In the field of financial analysis, the P-value is a statistical measure that helps determine the significance of a particular result or finding. It is a crucial tool for making informed decisions and drawing meaningful conclusions from data.

The P-value represents the probability of obtaining a result as extreme as, or more extreme than, the observed data, assuming that the null hypothesis is true. The null hypothesis is a statement that assumes there is no significant difference or relationship between variables.

By calculating the P-value, analysts can assess whether the observed data provides enough evidence to reject the null hypothesis and support an alternative hypothesis. If the P-value is below a predetermined significance level (usually 0.05), it suggests that the observed data is statistically significant and the null hypothesis can be rejected.

Financial analysts use the P-value to evaluate the significance of various factors in their analysis. For example, they can determine the impact of interest rates on stock prices, the effectiveness of a marketing campaign on sales, or the relationship between a company’s financial ratios and its profitability.

Step-by-Step Guide to Calculating P-Value

In statistical hypothesis testing, the p-value is a measure of the evidence against the null hypothesis. It helps determine the statistical significance of the results obtained from a study or experiment. Calculating the p-value involves several steps, which are outlined below:

Step 1: Define the Null and Alternative Hypotheses

The first step in calculating the p-value is to clearly define the null hypothesis (H0) and the alternative hypothesis (Ha). The null hypothesis represents the default assumption or the absence of an effect, while the alternative hypothesis represents the claim or the presence of an effect.

Step 2: Select the Appropriate Test Statistic

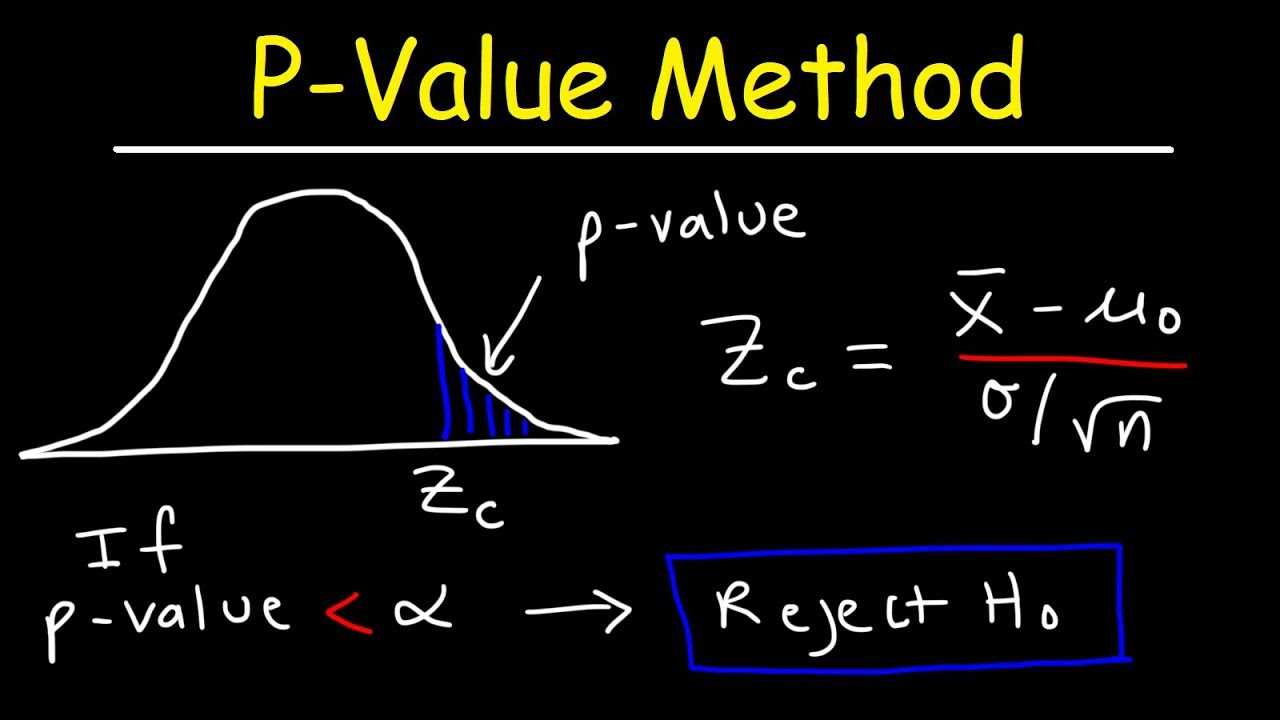
Once the hypotheses are defined, the next step is to select the appropriate test statistic based on the nature of the data and the research question. Common test statistics include t-tests, chi-square tests, and F-tests, among others.

Step 3: Determine the Distribution of the Test Statistic

After selecting the test statistic, it is necessary to determine the distribution of the test statistic under the null hypothesis. This distribution is used to calculate the p-value.

Step 4: Calculate the Test Statistic

Using the observed data, calculate the test statistic based on the chosen formula or method. The test statistic quantifies the difference between the observed data and what would be expected under the null hypothesis.

Step 5: Determine the P-Value

Once the test statistic is calculated, determine the p-value by comparing the test statistic to the distribution of the test statistic under the null hypothesis. The p-value represents the probability of obtaining a test statistic as extreme as, or more extreme than, the observed test statistic, assuming the null hypothesis is true.

Step 6: Interpret the Results

Finally, interpret the results by comparing the calculated p-value to a predetermined significance level (alpha). If the p-value is less than alpha, the results are considered statistically significant, and the null hypothesis is rejected in favor of the alternative hypothesis. If the p-value is greater than alpha, the results are not statistically significant, and the null hypothesis is not rejected.

By following these six steps, researchers can calculate the p-value and determine the statistical significance of their findings. It is important to note that the p-value should not be the sole basis for drawing conclusions, but rather used in conjunction with other relevant information and considerations.

Interpreting P-Value Results and Determining Statistical Significance

When conducting a statistical analysis, the p-value is a crucial measure that helps determine the significance of the results. It provides information about the likelihood of obtaining the observed data under the null hypothesis. Interpreting the p-value correctly is essential for making informed decisions and drawing valid conclusions in financial analysis.

Typically, a significance level (α) is chosen before conducting the analysis. The most common value for α is 0.05, which corresponds to a 5% chance of rejecting the null hypothesis when it is true. If the p-value is less than the chosen significance level, the null hypothesis is rejected, and the results are considered statistically significant.

On the other hand, if the p-value is greater than the significance level, there is not enough evidence to reject the null hypothesis. This means that the observed data could have occurred by chance, and the results are not statistically significant.

It is important to note that statistical significance does not imply practical significance. Even if the results are statistically significant, they may not have a substantial impact in real-world scenarios. Therefore, it is crucial to consider the practical implications and context of the analysis when interpreting the p-value results.

When interpreting p-value results, it is also important to consider the sample size. A larger sample size can lead to smaller p-values, as it increases the power of the statistical test. Therefore, a small p-value does not necessarily imply a large effect size or practical significance.

Term	Definition
p-value	A probability value that represents the likelihood of obtaining the observed data under the null hypothesis.
Significance level (α)	The predetermined threshold used to determine whether the p-value is statistically significant.
Statistical significance	The rejection of the null hypothesis based on the p-value being lower than the chosen significance level.
Practical significance	The real-world impact or importance of the results, regardless of statistical significance.
Sample size	The number of observations or data points used in the analysis, which can affect the p-value.

Common Mistakes to Avoid in P-Value Calculation

1. Incorrect Hypothesis Testing

One of the most common mistakes is using the wrong hypothesis when conducting the p-value calculation. It is essential to clearly define the null and alternative hypotheses before performing the analysis. The null hypothesis represents the assumption of no effect or no difference, while the alternative hypothesis represents the opposite. Using the wrong hypothesis can lead to incorrect p-value calculations and misleading results.

2. Improper Sample Size

Another common mistake is using an inadequate sample size for the analysis. A small sample size may not provide enough statistical power to detect significant effects accurately. Conversely, an excessively large sample size may lead to unnecessary costs and time-consuming data collection. It is crucial to determine an appropriate sample size based on the desired level of statistical power and significance.

3. Violation of Assumptions

Many statistical tests require certain assumptions to be met for accurate p-value calculations. Violating these assumptions can lead to biased results and incorrect interpretations. Some common assumptions include the normality of the data, independence of observations, and homogeneity of variances. It is essential to check and satisfy these assumptions before conducting the analysis.

4. Multiple Testing

Performing multiple tests without adjusting for multiple comparisons is another common mistake. When conducting multiple tests, the probability of obtaining a significant result by chance increases. To account for this, various methods, such as Bonferroni correction or false discovery rate control, can be used to adjust the p-values. Failing to adjust for multiple testing can lead to an inflated number of false positives.

5. Misinterpretation of p-Value

Misinterpreting the p-value is a common error that can lead to incorrect conclusions. The p-value represents the probability of obtaining the observed data or more extreme results under the null hypothesis. It does not provide information about the effect size or the practical significance of the results. Therefore, it is essential to interpret the p-value in conjunction with other statistical measures and consider the context of the analysis.

6. Publication Bias

Publication bias occurs when studies with statistically significant results are more likely to be published than those with non-significant results. This bias can lead to an overestimation of the true effect size and an inflated number of significant findings in the literature. It is crucial to consider and address publication bias when interpreting the p-value and the overall significance of the results.

Mistake	Impact	Prevention
Incorrect Hypothesis Testing	Incorrect conclusions	Clearly define null and alternative hypotheses
Improper Sample Size	Low statistical power or unnecessary costs	Determine appropriate sample size based on desired power
Violation of Assumptions	Biased results	Check and satisfy assumptions before analysis
Multiple Testing	Inflated false positives	Adjust p-values for multiple comparisons
Misinterpretation of p-Value	Incorrect conclusions	Interpret p-value in conjunction with other measures
Publication Bias	Overestimation of effect size	Consider and address publication bias

Advanced Techniques for P-Value Calculation and Significance Testing

1. Bootstrapping: Bootstrapping is a resampling technique that involves creating multiple samples from the original data set. By randomly selecting observations with replacement, bootstrapping allows for the estimation of the sampling distribution of a statistic. This technique is particularly useful when the assumptions of traditional statistical tests are not met, such as when the data is non-normal or the sample size is small. Bootstrapping can provide more robust p-values and confidence intervals.

3. Bayesian Methods: Bayesian methods offer an alternative approach to hypothesis testing by incorporating prior knowledge and beliefs about the parameters of interest. Unlike frequentist methods that focus on the probability of observing the data given a hypothesis, Bayesian methods provide a posterior probability distribution for the hypothesis given the data. This allows for the direct calculation of the probability of the hypothesis being true, given the observed data. Bayesian methods can be especially useful when dealing with complex models or when incorporating prior information is important.

4. Monte Carlo Simulation: Monte Carlo simulation involves generating random samples from a probability distribution to estimate the p-value. By repeatedly sampling from the distribution and calculating the test statistic, the p-value can be approximated. Monte Carlo simulation is particularly useful when the distribution of the test statistic is unknown or when analytical solutions are not feasible. This technique allows for more flexible and accurate p-value estimation.

Advanced Technique	Application
Bootstrapping	Non-normal data, small sample sizes
Permutation Testing	Violated assumptions, small sample sizes
Bayesian Methods	Complex models, incorporating prior information
Monte Carlo Simulation	Unknown distribution, infeasible analytical solutions
Multiple Testing Corrections	Multiple hypothesis tests