Exploring the Functionality of Kappa and its Applications
Kappa is a statistical measure that is widely used in various fields to assess the level of agreement between two or more raters or observers. It provides a quantitative measure of the extent to which the raters agree beyond what would be expected by chance alone.
One of the key functionalities of kappa is its ability to account for chance agreement. This is particularly important when dealing with subjective judgments or assessments, where there may be a certain degree of variability in the ratings. Kappa takes into consideration the possibility of agreement occurring by chance and adjusts the agreement measure accordingly.
Kappa is commonly used in fields such as psychology, medicine, and social sciences, where subjective judgments and assessments are prevalent. For example, in psychology, kappa can be used to assess the inter-rater reliability of diagnostic criteria for mental disorders. In medicine, kappa can be used to evaluate the agreement between different radiologists in interpreting medical images.
Furthermore, kappa can also be used to compare the agreement between different methods or techniques. For instance, in a study comparing two different measurement instruments, kappa can be used to determine the level of agreement between the two methods. This can be particularly useful in fields such as market research or quality control, where different measurement techniques are often employed.
Measuring Kappa: Methods and Techniques

Cohen’s Kappa
Cohen’s kappa is one of the most widely used methods for measuring kappa. It is a statistical measure that assesses the agreement between two raters or observers. Cohen’s kappa takes into account both the observed agreement and the agreement that could be expected by chance.
To calculate Cohen’s kappa, the observed agreement and the agreement expected by chance are compared. The formula for Cohen’s kappa is:
Where:
- K is the value of Cohen’s kappa
- Po is the observed agreement
- Pe is the agreement expected by chance
Cohen’s kappa ranges from -1 to 1, where a value of 1 indicates perfect agreement, 0 indicates agreement by chance, and -1 indicates complete disagreement.
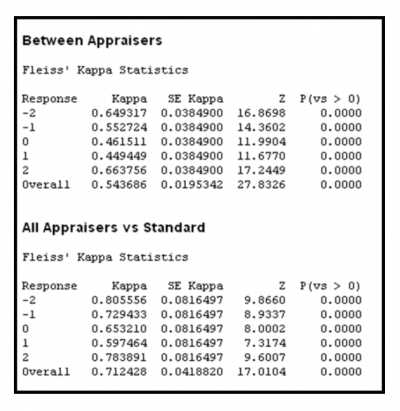
Fleiss’ Kappa
Fleiss’ kappa is another commonly used method for measuring kappa. It is an extension of Cohen’s kappa and is used when there are more than two raters or observers. Fleiss’ kappa takes into account the agreement among multiple raters and provides a measure of interrater reliability.
The formula for Fleiss’ kappa is similar to Cohen’s kappa, but it takes into account the agreement among multiple raters:
Where:
- K is the value of Fleiss’ kappa
- Po is the observed agreement
- Pe is the agreement expected by chance
Like Cohen’s kappa, Fleiss’ kappa ranges from -1 to 1, with 1 indicating perfect agreement, 0 indicating agreement by chance, and -1 indicating complete disagreement.
Interpretation of Kappa Values
Interpreting kappa values depends on the context and the field of study. Generally, kappa values above 0.8 are considered to indicate excellent agreement, values between 0.6 and 0.8 indicate good agreement, values between 0.4 and 0.6 indicate moderate agreement, and values below 0.4 indicate poor agreement.
It is important to note that kappa is just one measure of agreement and should be interpreted in conjunction with other relevant factors and considerations.
Options and Derivatives: Expanding the Kappa Framework
Options and derivatives are financial instruments that derive their value from an underlying asset, such as stocks, bonds, or commodities. These instruments play a crucial role in modern financial markets, providing investors with opportunities to hedge against risk, speculate on price movements, and diversify their portfolios.
One of the key aspects of expanding the Kappa framework is the development of advanced measurement techniques. Traditional methods, such as Black-Scholes model, provide a good starting point for valuing options and derivatives. However, they have limitations and may not accurately capture the complexities of real-world market conditions.
Additionally, the functionality of options and derivatives within the Kappa framework can be expanded by incorporating more sophisticated trading strategies. This includes strategies such as delta hedging, gamma scalping, and volatility trading. By incorporating these strategies, investors can enhance their ability to manage risk, generate profits, and optimize their portfolios.

Emily Bibb simplifies finance through bestselling books and articles, bridging complex concepts for everyday understanding. Engaging audiences via social media, she shares insights for financial success. Active in seminars and philanthropy, Bibb aims to create a more financially informed society, driven by her passion for empowering others.
