Type 1 Error: Definition, False Positives, and Examples

Type 1 Error: Definition

When conducting a statistical test, researchers set a significance level, denoted as α (alpha), which represents the probability of making a Type 1 error. Typically, a significance level of 0.05 or 5% is used, meaning that there is a 5% chance of rejecting the null hypothesis when it is true.

A false positive, or Type 1 error, can occur in various fields, including medicine, psychology, and quality control. It is important to understand false positives because they can lead to incorrect conclusions and decisions.

For example, in medical testing, a false positive result can lead to unnecessary treatments or surgeries, causing harm to the patient. In quality control, a false positive can result in the rejection of a batch of products that are actually within the acceptable limits, leading to financial losses for the company.

To minimize the risk of Type 1 errors, researchers can increase the sample size, use more rigorous statistical methods, or adjust the significance level. However, it is important to strike a balance between minimizing Type 1 errors and avoiding Type 2 errors, which occur when a true effect or relationship is not detected.

Examples of Type 1 Error in Math and Statistics

There are several examples of Type 1 errors in math and statistics. One common example is a hypothesis test for the mean of a population. If the null hypothesis states that the mean is equal to a certain value, and the alternative hypothesis states that the mean is not equal to that value, a Type 1 error occurs when the null hypothesis is rejected even though the true population mean is actually equal to the specified value.

Another example is a hypothesis test for the correlation coefficient. If the null hypothesis states that there is no correlation between two variables, and the alternative hypothesis states that there is a correlation, a Type 1 error occurs when the null hypothesis is rejected even though there is no true correlation between the variables.

False positives are a common phenomenon in various fields, including math and statistics. It refers to a situation where a test or analysis incorrectly identifies something as true or positive when it is actually false or negative. In other words, it is a type of error that occurs when a hypothesis or claim is mistakenly accepted or validated, even though it is not true.

False positives can have significant consequences, depending on the context in which they occur. In medical testing, for example, a false positive result can lead to unnecessary treatments or surgeries, causing physical and emotional distress to patients. In criminal justice, a false positive identification can result in the wrongful conviction of an innocent person.

Causes of False Positives

There are several factors that can contribute to the occurrence of false positives:

1. Sensitivity of the Test: Some tests or analyses may have a high sensitivity, meaning they are designed to detect even the smallest traces of a particular condition or characteristic. While this can be beneficial in detecting true positives, it also increases the likelihood of false positives.
2. Sample Size: The size of the sample being tested can influence the likelihood of false positives. Smaller sample sizes may be more prone to producing false positives due to the limited amount of data available for analysis.
3. Statistical Significance: The threshold for determining statistical significance can also impact the occurrence of false positives. If the threshold is set too low, it may increase the chances of accepting false positives.

Minimizing False Positives

While it may not be possible to completely eliminate false positives, there are strategies that can help minimize their occurrence:

1. Validation and Replication: It is important to validate and replicate the results of tests or analyses to ensure their accuracy. Multiple independent tests can help confirm the presence of true positives and reduce the likelihood of false positives.
2. Adjusting Statistical Thresholds: Adjusting the statistical thresholds for determining significance can help control the rate of false positives. By setting a higher threshold, the chances of accepting false positives can be reduced.
3. Improving Test Sensitivity: Enhancing the sensitivity of tests or analyses can help reduce false positives. However, it is essential to strike a balance between sensitivity and specificity to avoid an excessive number of false positives or false negatives.

Examples of Type 1 Error in Math and Statistics

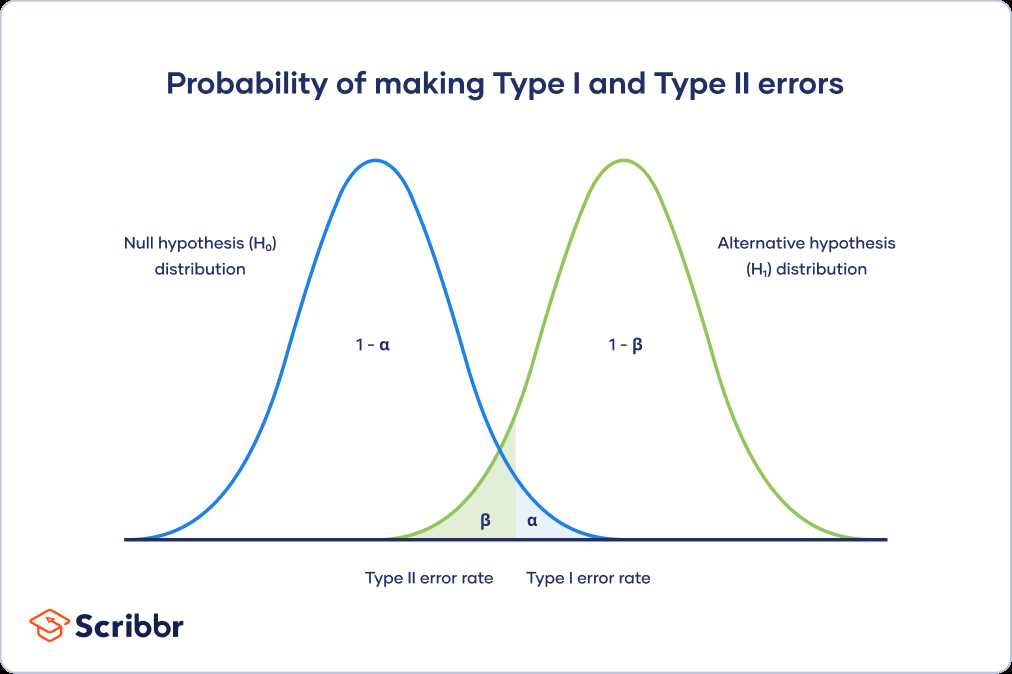
Here are some examples of type 1 error in math and statistics:

Example	Description
Medical Testing	In medical testing, type 1 error can occur when a patient is diagnosed with a disease or condition, even though they are actually healthy. This can lead to unnecessary treatments and interventions.
Quality Control	In quality control processes, type 1 error can happen when a product is deemed defective, even though it meets the required standards. This can result in wasted resources and unnecessary rejections.
Criminal Justice	In criminal justice, type 1 error can occur when an innocent person is wrongly convicted of a crime. This can have severe consequences for the individual and the justice system.
Market Research	In market research, type 1 error can happen when a false positive is identified, indicating that a particular product or service will be successful, leading to potentially poor business decisions.
Scientific Research	In scientific research, type 1 error can occur when a researcher falsely concludes that there is a significant relationship or effect, leading to incorrect conclusions and wasted resources.