Key Components of the Black-Scholes Model
The Black-Scholes model takes into account several key components:
| Component | Description |
|---|---|
| Stock Price | The current market price of the underlying stock. This is a crucial input in the Black-Scholes formula as it determines the potential profitability of the option. |
| Strike Price | |
| Time to Expiration | The remaining time until the option’s expiration date. The longer the time to expiration, the higher the probability of the option being profitable. This parameter is a crucial factor in the Black-Scholes formula. |
| Volatility | The measure of the stock’s price fluctuations over time. Higher volatility implies a higher potential for price movement, which increases the value of the option. Volatility is a critical input in the Black-Scholes formula. |
| Risk-Free Interest Rate | The interest rate at which an investor can borrow or lend money without any risk. It is an essential component in the Black-Scholes model as it determines the present value of the option’s future cash flows. |
| Dividends | The cash payments made by a company to its shareholders. If a stock pays dividends, it affects the price of the option. The Black-Scholes formula accounts for dividends to calculate the option’s value accurately. |
Calculating Option Prices with the Black-Scholes Formula
To calculate option prices using the Black-Scholes formula, several key inputs are required:
1. Underlying Asset Price
The current market price of the underlying asset, such as a stock or a commodity, is a crucial input in the Black-Scholes model. This price represents the value of the asset on which the option is based.
2. Strike Price
3. Time to Expiration
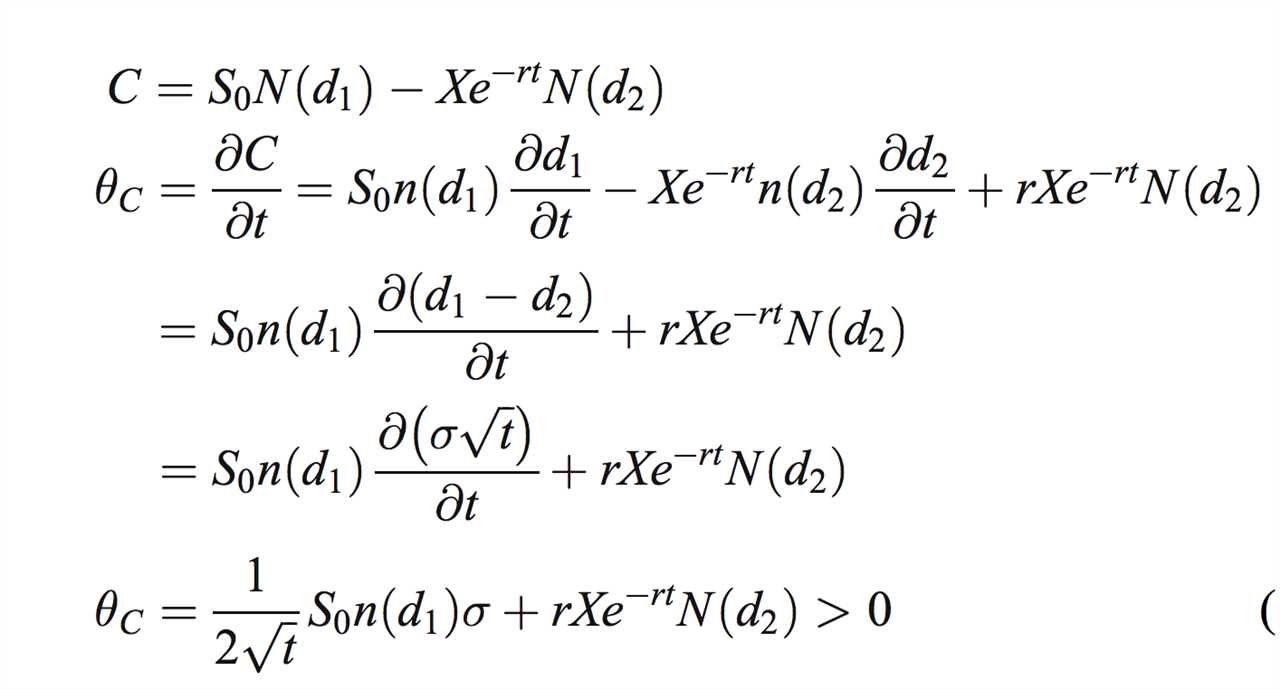
The time remaining until the option’s expiration is another critical input in the Black-Scholes formula. It represents the period during which the option holder can exercise their right to buy or sell the underlying asset.
4. Volatility
5. Risk-Free Interest Rate
The risk-free interest rate is the rate of return on a risk-free investment, such as a government bond. It is an essential input in the Black-Scholes formula as it represents the opportunity cost of tying up capital in the option rather than investing it elsewhere.
The Black-Scholes formula calculates the option price by considering the present value of the expected future cash flows from the option. It accounts for the probability of different future price scenarios and discounts them to their present value using the risk-free interest rate.
It is important to note that the Black-Scholes formula assumes certain conditions, such as constant volatility and a continuous trading environment. These assumptions may not always hold true in real-world situations, and therefore, the calculated option prices may deviate from the actual market prices.
Limitations and Assumptions of the Black-Scholes Model
The Black-Scholes model, developed by economists Fischer Black and Myron Scholes in 1973, revolutionized the field of options pricing and derivatives trading. However, like any model, it is based on a set of assumptions and has certain limitations that must be considered.
1. Efficient Market Hypothesis: The Black-Scholes model assumes that financial markets are efficient, meaning that all relevant information is immediately reflected in asset prices. This assumption may not hold true in real-world markets, where factors such as market manipulation or information asymmetry can affect prices.
2. Constant Volatility: The model assumes that the volatility of the underlying asset’s returns is constant over the life of the option. In reality, volatility can change over time, leading to inaccurate pricing predictions. Traders and investors must constantly monitor and adjust their volatility assumptions to account for market conditions.
3. Continuous Trading: The Black-Scholes model assumes that trading is continuous, with no restrictions on the buying and selling of assets. In reality, trading may be limited by factors such as market hours, liquidity constraints, or regulatory restrictions. These limitations can affect the accuracy of the model’s predictions.
4. No Transaction Costs: The model assumes that there are no transaction costs, such as brokerage fees or taxes, associated with trading options. In practice, these costs can significantly impact the profitability of options trading strategies and should be taken into account when using the Black-Scholes model.
5. Normal Distribution of Returns: The Black-Scholes model assumes that the returns of the underlying asset follow a normal distribution. However, in reality, asset returns often exhibit skewness and kurtosis, meaning that they are not perfectly normally distributed. This can lead to inaccurate pricing predictions, especially in extreme market conditions.
6. No Dividends: The model assumes that the underlying asset does not pay dividends during the life of the option. In reality, many stocks and other assets do pay dividends, which can affect the pricing and profitability of options. Adjustments must be made to the model to account for dividend payments.
7. Risk-Neutral Assumption: The Black-Scholes model assumes that investors are risk-neutral, meaning that they do not consider the riskiness of the underlying asset when making investment decisions. In reality, investors have different risk preferences, and their perception of risk can affect option pricing. Adjustments may be necessary to account for risk aversion.
Applications and Importance of the Black-Scholes Model

The Black-Scholes model, developed by economists Fischer Black and Myron Scholes in 1973, revolutionized the field of finance by providing a mathematical framework for pricing options and other derivatives. This model has since become a cornerstone of modern financial theory and is widely used by investors, traders, and financial institutions around the world.
By using the Black-Scholes model, investors can make informed decisions about buying or selling options. For example, if the calculated fair value of an option is higher than its market price, an investor may consider buying the option as it is potentially undervalued. On the other hand, if the calculated fair value is lower than the market price, an investor may consider selling the option as it is potentially overvalued.
Another important application of the Black-Scholes model is in risk management. Financial institutions use the model to assess and manage the risks associated with their options and derivatives portfolios. By calculating the fair values of options and measuring their sensitivities to various factors, such as changes in the underlying asset price or volatility, institutions can determine the potential impact of these factors on their overall portfolio value. This allows them to hedge their positions and mitigate potential losses.

Emily Bibb simplifies finance through bestselling books and articles, bridging complex concepts for everyday understanding. Engaging audiences via social media, she shares insights for financial success. Active in seminars and philanthropy, Bibb aims to create a more financially informed society, driven by her passion for empowering others.
