Hull-White Model Explained: The Mechanics

Hull-White Model Explained

The Hull-White model is a popular interest rate model used in finance to price and hedge interest rate derivatives. It was developed by John Hull and Alan White in 1990 and is an extension of the Vasicek model. The model assumes that the short-term interest rate follows a mean-reverting process and incorporates stochastic volatility.

Mechanics of the Hull-White Model

In addition to mean reversion, the Hull-White model incorporates stochastic volatility, which means that the volatility of interest rates is not constant but varies over time. This is an important feature as it allows the model to capture the observed volatility smile in the market, where options with different strike prices have different implied volatilities.

The Hull-White model is a forward-rate model, meaning it models the evolution of future interest rates. It does this by specifying a stochastic process for the short-term interest rate and then using this process to calculate the prices of interest rate derivatives such as swaps and caps/floors.

Advantages and Limitations

One of the advantages of the Hull-White model is its flexibility. It allows for the modeling of various interest rate environments, including both mean-reverting and non-mean-reverting interest rates. This makes it suitable for a wide range of applications in pricing and risk management.

However, the Hull-White model also has its limitations. One limitation is that it assumes that interest rates follow a continuous-time process, which may not hold true in practice. Additionally, the model requires the estimation of several parameters, which can be challenging and may introduce uncertainty into the pricing and risk management process.

Despite its limitations, the Hull-White model remains a widely used and influential model in the field of interest rate derivatives. Its ability to capture both mean reversion and stochastic volatility makes it a valuable tool for pricing and hedging these complex financial instruments.

The Hull-White model is a popular interest rate model used in financial markets to price and hedge interest rate derivatives. It is a one-factor model that takes into account the mean reversion of interest rates and the volatility of interest rate movements.

Mean Reversion

One of the key features of the Hull-White model is its incorporation of mean reversion. This means that interest rates tend to move towards a long-term average over time. The model assumes that interest rates follow a stochastic process, and the mean reversion parameter determines how quickly rates revert to the long-term average.

The mean reversion feature of the Hull-White model is important because it helps capture the behavior of interest rates in real-world markets. By incorporating mean reversion, the model can better reflect the tendency of interest rates to fluctuate around a certain level.

Volatility

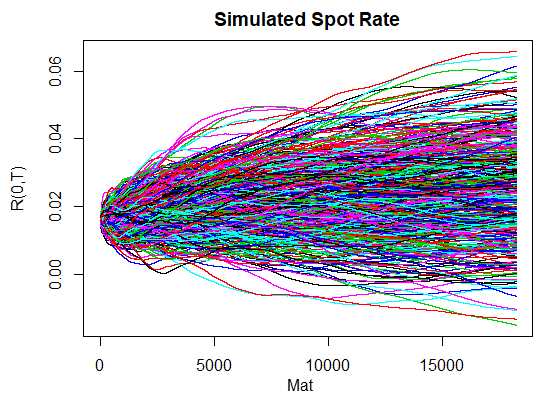
Another important aspect of the Hull-White model is its consideration of interest rate volatility. Volatility refers to the magnitude of price fluctuations in a financial instrument. In the case of interest rates, volatility represents the uncertainty or variability in rate movements.

The Hull-White model assumes that interest rate volatility is a function of time and the level of interest rates. It uses a volatility parameter to capture this relationship. By incorporating volatility, the model can account for the fluctuations and uncertainty in interest rate movements.

STRATEGY & EDUCATION

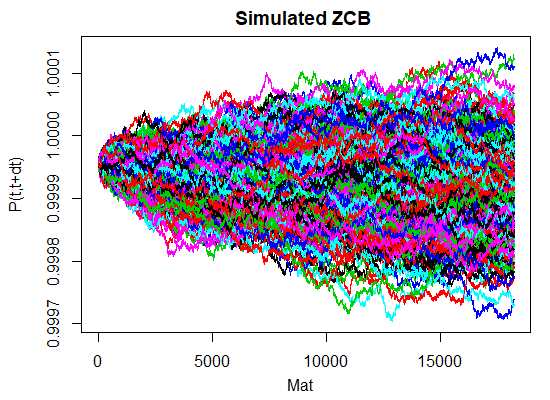
What is the Hull-White Model?

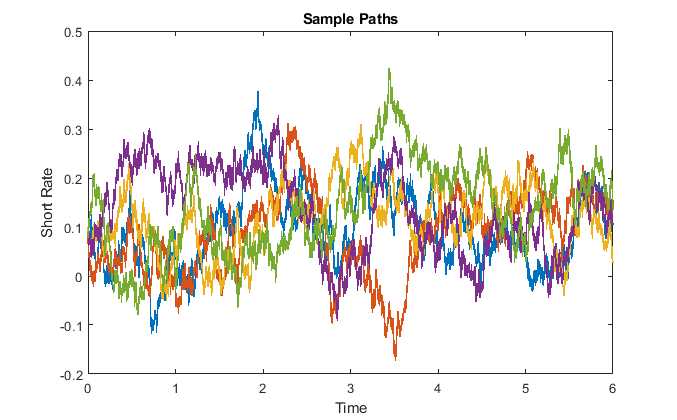
The Hull-White model is a one-factor model that describes the evolution of interest rates over time. It assumes that interest rates follow a mean-reverting process, meaning that they tend to revert to a long-term average. This model takes into account the term structure of interest rates and allows for the incorporation of market data to calibrate the model parameters.

The mechanics of the Hull-White model involve several key components. Firstly, the model assumes that the short-term interest rate follows a stochastic process, which is governed by a stochastic differential equation. This equation takes into account the current interest rate, the long-term mean interest rate, and a volatility parameter.

Secondly, the model incorporates the term structure of interest rates by using a set of yield curves, which represent the relationship between interest rates and the time to maturity of a bond. These yield curves are used to calibrate the model and determine the parameters that best fit the observed market data.

Lastly, the Hull-White model allows for the pricing of interest rate derivatives, such as interest rate swaps and options. By simulating the future evolution of interest rates based on the model parameters, the model can be used to calculate the present value of future cash flows associated with these derivatives.

STRATEGY & EDUCATION

The Hull-White Model is a one-factor model that assumes interest rates follow a mean-reverting process. This means that interest rates tend to move towards a long-term average over time. The model takes into account the current interest rate, the mean-reversion speed, and the volatility of interest rates to calculate future interest rate movements.

One of the key features of the Hull-White Model is its ability to capture the term structure of interest rates. The term structure refers to the relationship between interest rates of different maturities. By incorporating the term structure, the model can accurately price interest rate derivatives with different maturities and provide insights into the yield curve.

The Hull-White Model is widely used by financial institutions for various purposes. It is commonly used to price interest rate options, such as caps, floors, and swaptions. The model can also be used to simulate interest rate scenarios and assess the impact of interest rate movements on a portfolio’s value. Additionally, the Hull-White Model is often used in risk management to hedge against interest rate risk.