What is Continuous Compounding?
Continuous compounding is a concept in finance that refers to the process of calculating interest or returns on an investment continuously, rather than at discrete intervals. It is a mathematical model that assumes that interest is compounded infinitely often over a given period of time.
In traditional compounding, interest or returns are calculated and added to the principal at specific intervals, such as annually, semi-annually, quarterly, or monthly. However, continuous compounding assumes that the interest is added continuously, resulting in a higher overall return.
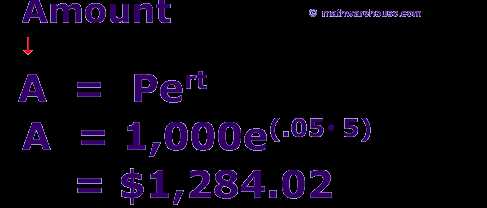
The formula for continuous compounding is given by the equation:
A = P * e^(rt)
Where:
- A is the final amount
- P is the principal amount
- e is the mathematical constant approximately equal to 2.71828
- r is the interest rate
- t is the time period
Continuous compounding is commonly used in various financial applications, including dividend stocks. By applying continuous compounding, investors can calculate the future value of their investments and make informed decisions regarding their portfolio.
Definition and Formula

Continuous compounding is a concept in finance that refers to the process of calculating interest or investment growth continuously over time. Unlike simple or compound interest, which is calculated at specific intervals, continuous compounding assumes that interest is constantly being added to the principal amount.
The formula for continuous compounding is given by:
A = P * e^(rt)
Where:
- A is the final amount or value of the investment
- P is the principal amount or initial investment
- e is the mathematical constant approximately equal to 2.71828
- r is the annual interest rate (expressed as a decimal)
- t is the time period in years
Example:
Let’s say you invest $10,000 in a dividend stock that offers a 5% annual interest rate. Using the continuous compounding formula, we can calculate the value of the investment after 5 years:
A = 10000 * e^(0.05 * 5)
Using a calculator or a spreadsheet, we can find that the value of the investment after 5 years is approximately $12,749.68.
Continuous compounding is a concept in finance that refers to the process of calculating interest or growth on an investment continuously over time. Unlike simple or compound interest, which are calculated at specific intervals, continuous compounding takes into account infinitesimally small time intervals, resulting in a more accurate and precise calculation.
The formula for continuous compounding is given by:
| A | = | P | e | r | t |
Where:
- A is the final amount
- P is the principal amount
- e is the mathematical constant approximately equal to 2.71828
- r is the interest rate
- t is the time period
Continuous compounding is particularly useful when dealing with investments that generate income or dividends at regular intervals, such as dividend stocks. By using continuous compounding, investors can accurately calculate the future value of their investment, taking into account the continuous reinvestment of dividends.
Continuous compounding is widely used in financial calculations, especially in the field of investments. It provides a more accurate representation of the growth potential of an investment and allows investors to make informed decisions based on realistic projections.
How Continuous Compounding Works and Its Benefits
Continuous compounding is a powerful concept in finance that allows for the exponential growth of investments. It works by reinvesting the interest earned on an investment continuously, rather than at regular intervals. This means that the interest is added to the principal amount continuously, allowing for compounding to occur more frequently.
The formula for continuous compounding is given by the equation A = P * e^(rt), where A is the final amount, P is the principal amount, e is the mathematical constant approximately equal to 2.71828, r is the interest rate, and t is the time period.
Continuous compounding also allows for greater flexibility in investment strategies. Since the interest is reinvested continuously, investors have the option to withdraw or reinvest the accumulated interest at any time. This can be particularly advantageous in dividend stocks, where the dividends can be reinvested to purchase additional shares, further increasing the potential for growth.
Another advantage of continuous compounding is that it eliminates the need for regular compounding intervals. With traditional compounding methods, such as annual or quarterly compounding, the interest is only added to the principal at specific intervals. Continuous compounding removes this limitation, allowing for a more dynamic and efficient growth of the investment.
Application of Continuous Compounding in Dividend Stocks

Continuous compounding can be a valuable tool for investors looking to maximize their returns in dividend stocks. By reinvesting dividends and taking advantage of the compounding effect, investors can potentially see their investment grow at an accelerated rate.
Overall, continuous compounding can be a powerful strategy for investors in dividend stocks. By reinvesting dividends and taking advantage of the compounding effect, investors can potentially see their investment grow at an accelerated rate, generate a passive income stream, and benefit from long-term capital appreciation.

Emily Bibb simplifies finance through bestselling books and articles, bridging complex concepts for everyday understanding. Engaging audiences via social media, she shares insights for financial success. Active in seminars and philanthropy, Bibb aims to create a more financially informed society, driven by her passion for empowering others.
