The T-Distribution In Probability And Its Practical Applications

What is the T-Distribution?

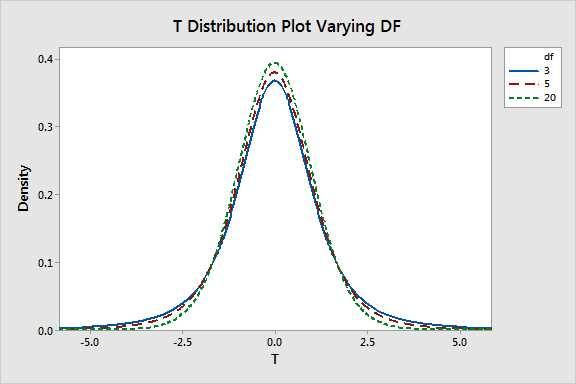
The T-distribution is often used in hypothesis testing and confidence interval estimation. In hypothesis testing, it helps determine whether the difference between sample means is statistically significant. In confidence interval estimation, it provides a range of values within which the population parameter is likely to fall.

One of the key properties of the T-distribution is that it has fatter tails compared to the normal distribution. This means that extreme values are more likely to occur in the T-distribution, making it more robust to outliers. This is particularly useful when dealing with small sample sizes, where outliers can have a larger impact on the results.

In practical applications, the T-distribution is commonly used in fields such as statistics, economics, and engineering. It allows researchers to make inferences about population parameters based on limited sample data. For example, in medical research, the T-distribution can be used to compare the effectiveness of different treatments based on small sample sizes.

Properties and Characteristics of the T-Distribution

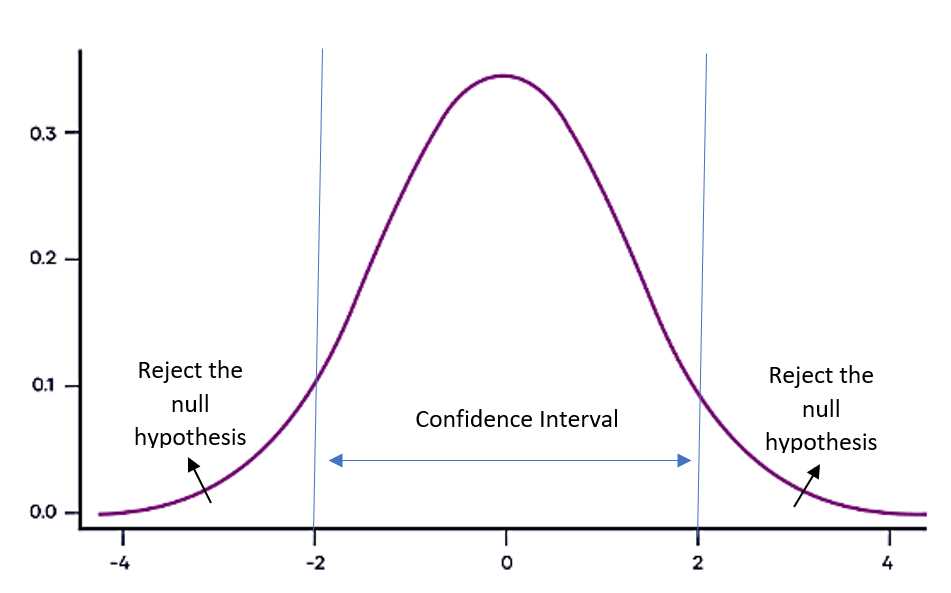
Here are some important properties and characteristics of the T-distribution:

1. Symmetry:

The T-distribution is symmetric around its mean, which is usually zero. This means that the probability of obtaining a positive value is the same as obtaining a negative value.

2. Degrees of Freedom:

3. Tails:

The T-distribution has heavier tails compared to the normal distribution. This means that there is a higher probability of observing extreme values in the T-distribution compared to the normal distribution.

4. Confidence Intervals:

5. Hypothesis Testing:

The T-distribution is also used in hypothesis testing, where we compare sample statistics to population parameters to make inferences about the population. The T-distribution allows us to calculate the probability of obtaining a certain sample statistic under the null hypothesis.

Overall, the T-distribution is a valuable tool in statistics, particularly when dealing with small sample sizes or unknown population standard deviations. Its properties and characteristics make it suitable for various statistical analyses and inference methods.

Practical Applications of the T-Distribution

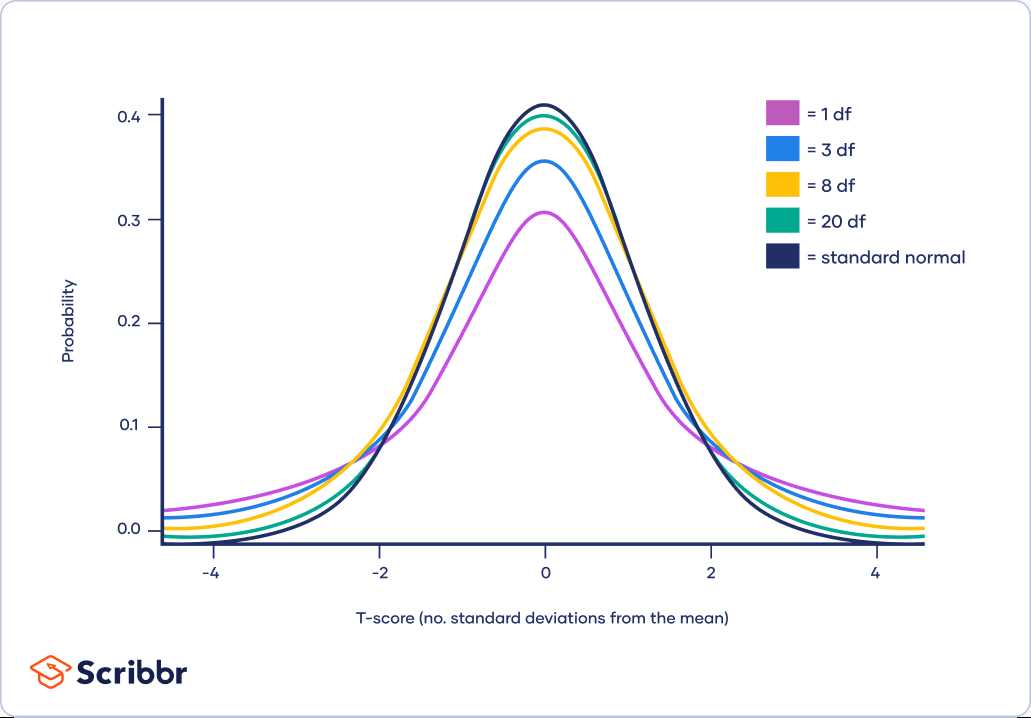
One of the main applications of the T-distribution is in hypothesis testing. Hypothesis testing involves making inferences about a population based on a sample. The T-distribution is used to calculate the critical values and p-values necessary for hypothesis testing when the sample size is small or when the population standard deviation is unknown. This makes it particularly useful in situations where the sample size is limited or when dealing with data that does not follow a normal distribution.

In finance, the T-distribution is often used in estimating the value at risk (VaR) of a portfolio. VaR is a measure of the maximum potential loss that a portfolio may incur over a given time period. By using the T-distribution, financial analysts can account for the uncertainty and variability in the returns of different assets in the portfolio. This helps in making informed decisions about risk management and asset allocation.

In medicine, the T-distribution is used in clinical trials to determine the efficacy of a new drug or treatment. By comparing the mean values of a control group and a treatment group, researchers can assess whether the treatment has a significant effect. The T-distribution allows for the calculation of confidence intervals and p-values, which help in drawing conclusions about the effectiveness of the treatment.

In engineering, the T-distribution is used in quality control and process improvement. It is often used to analyze data from production processes and determine whether they are within acceptable limits. By calculating confidence intervals and conducting hypothesis tests using the T-distribution, engineers can identify areas for improvement and make informed decisions to optimize the manufacturing process.