Degrees of Freedom in Statistics: Formula and Example

Degrees of Freedom in Statistics: Formula and Example [ECONOMICS catname]

In statistics, degrees of freedom refer to the number of independent pieces of information that are available to estimate a parameter or make an inference. It is an important concept in hypothesis testing and determining the variability of a statistical estimate.

Formula for Degrees of Freedom

The formula for calculating degrees of freedom depends on the specific statistical test or analysis being performed. However, a general formula can be used to understand the concept:

The total number of observations refers to the number of data points or individuals in the sample or population being analyzed. The number of restrictions refers to any constraints or limitations placed on the analysis.

Example of Degrees of Freedom Calculation

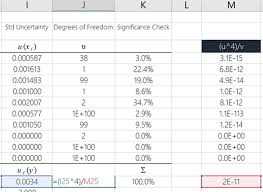
Let’s consider an example to understand how degrees of freedom are calculated. Suppose we have a sample of 50 individuals and we want to estimate the mean height of the population. We know that the sample mean is an unbiased estimator of the population mean.

Statistic	Degrees of Freedom
t-test
Chi-square test
F-test

In statistics, degrees of freedom refers to the number of independent pieces of information that are available to estimate a parameter or make an inference about a population. It is a concept that is crucial in many statistical tests and analyses.

When conducting statistical analyses, researchers often have a limited amount of data available to make inferences about a larger population. Degrees of freedom help determine the number of values that are free to vary in the calculation of a statistic.

For example, let’s say we have a sample of 10 individuals and we want to estimate the mean height of the population they come from. The sample mean is calculated by summing up the heights of the individuals and dividing by the sample size (10). However, since we are estimating the population mean based on a sample, we need to account for the fact that the sample mean is not likely to be exactly equal to the population mean.

In summary, degrees of freedom in statistics play a crucial role in estimating parameters and making inferences about populations based on limited data. They help determine the number of independent pieces of information available for statistical calculations and are essential in many statistical tests and analyses.

Calculating Degrees of Freedom: Formula and Example

In statistics, degrees of freedom (df) refers to the number of independent pieces of information that are available to estimate a parameter or make an inference. It is an important concept in hypothesis testing and determining the variability of a sample.

This means that we have 99 degrees of freedom to estimate the mean of the population based on our sample.

where “n” represents the sample size and “k” represents the number of predictors or independent variables. The subtraction of 1 accounts for the estimation of the intercept term.

For instance, if we have a sample size of 50 and a regression model with 2 predictors, the degrees of freedom would be:

This means that we have 47 degrees of freedom to estimate the coefficients of the regression model.

Statistical Test	Degrees of Freedom Formula
Mean
Regression
ANOVA