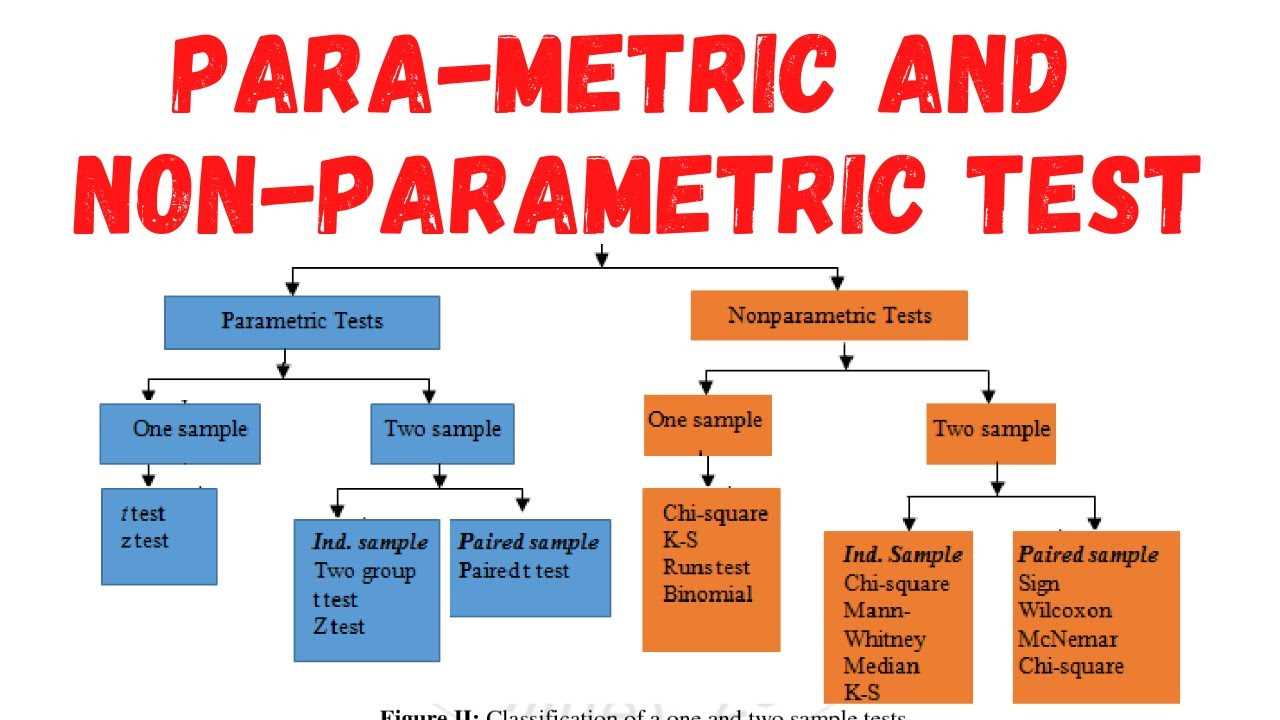
Types of Nonparametric Statistics
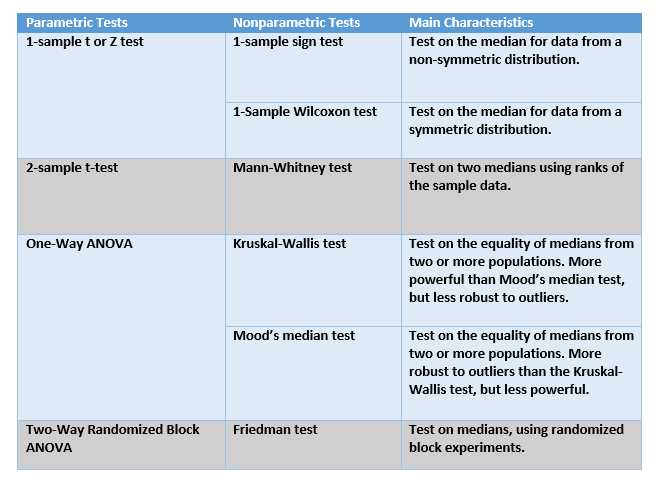
Nonparametric statistics are a type of statistical analysis that does not make any assumptions about the underlying distribution of the data. They are often used when the data does not meet the assumptions of parametric statistics, such as normality or homogeneity of variance.
There are several types of nonparametric statistics that can be used in financial analysis:
1. Mann-Whitney U Test:
The Mann-Whitney U test is used to compare the distributions of two independent groups. It is often used to determine if there is a significant difference between the returns of two investment portfolios or the performance of two companies.
2. Wilcoxon Signed-Rank Test:
The Wilcoxon signed-rank test is used to compare the distributions of two related groups. It is often used to determine if there is a significant difference between the returns of an investment portfolio before and after a specific event, such as a merger or acquisition.
3. Kruskal-Wallis Test:
The Kruskal-Wallis test is used to compare the distributions of three or more independent groups. It is often used to determine if there is a significant difference between the returns of multiple investment portfolios or the performance of multiple companies.
4. Friedman Test:
The Friedman test is used to compare the distributions of three or more related groups. It is often used to determine if there is a significant difference between the returns of multiple investment portfolios before and after a specific event.
5. Spearman’s Rank-Order Correlation:
Spearman’s rank-order correlation is used to measure the strength and direction of the relationship between two variables. It is often used to determine if there is a significant correlation between the returns of two investment portfolios or the performance of two companies.
These are just a few examples of the types of nonparametric statistics that can be used in financial analysis. By using nonparametric statistics, analysts can make robust and reliable conclusions without making assumptions about the underlying distribution of the data.
Examples of Nonparametric Statistics in Financial Analysis
Nonparametric statistics provide valuable tools for analyzing financial data when the underlying distribution is unknown or does not follow a specific parametric form. Here are some examples of how nonparametric statistics can be applied in financial analysis:
1. Sign Test
The sign test is a nonparametric test used to determine whether the median of a distribution is equal to a specified value. In financial analysis, the sign test can be used to assess the performance of a trading strategy by comparing the number of positive and negative returns. If the number of positive returns is significantly different from the number of negative returns, it may indicate that the trading strategy is effective.
2. Wilcoxon Signed-Rank Test
The Wilcoxon signed-rank test is a nonparametric test used to compare the medians of two related samples. In financial analysis, this test can be used to evaluate the performance of two investment strategies by comparing the returns generated by each strategy. If the medians of the returns are significantly different, it may indicate that one strategy outperforms the other.
Additionally, the Wilcoxon signed-rank test can be used to assess the significance of abnormal returns in event studies. By comparing the ranks of the abnormal returns to a null distribution, it is possible to determine whether the abnormal returns are statistically significant.
3. Mann-Whitney U Test

4. Kruskal-Wallis Test
The Kruskal-Wallis test is a nonparametric test used to compare the medians of three or more independent samples. In financial analysis, this test can be used to compare the performance of multiple investment strategies or to evaluate the impact of different market conditions on the returns of different asset classes.
These are just a few examples of how nonparametric statistics can be applied in financial analysis. By using these tests, analysts can make robust and reliable conclusions even when the assumptions of parametric tests are not met.

Emily Bibb simplifies finance through bestselling books and articles, bridging complex concepts for everyday understanding. Engaging audiences via social media, she shares insights for financial success. Active in seminars and philanthropy, Bibb aims to create a more financially informed society, driven by her passion for empowering others.
